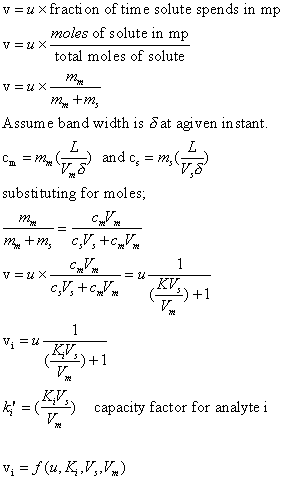
Velocity of migration of analytes:

This is a simple derivation of analyte migration velocity for a typical chromatographic system. Use with lecture presentation.

Let the linear velocity of the m.p. = u

Assume instantaneous equilibration and the number of moles of the analyte in m.p and s.p. respectively are m_m and m_s.

Noting that if no retention the analyte will move at u and the retention is due to partitioning into the s.p.

The velocity of an analyte, v, will then be,

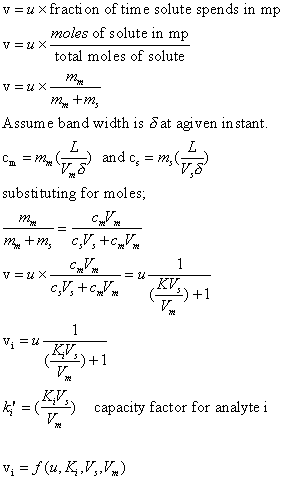
where, V_s, V_m, K are volume of the stationary phase, volume of the mobile phase, partition coefficient of the analyte and  L is the length of the column. The subscript i refers to the analyte i. For a given chromatographic system run under a constant set of physical conditions (which includes the materials of sp and mp), factors governing analyte migration velocity are the same for all analytes except K_i. Therefore each analyte will acquire a unique migration velocity depending on its partition coefficient.

Back to Contents  
Home