and 
. We often write fractional values in decimal form since it is a more compact form of writing a numerical value that represents a fractional value.Decimal Fractions
Terminating Decimals and Repeating Decimals
Explain the meaning of the values stated in the following sentence.
The gas can has a capacity of 4.17 gallons and weighs 3.4 pounds.
The values represent four and seventeen hundredths and three and four-tenths. In other words, the decimals are another way to write the mixed numbers and . We often write fractional values in decimal form since it is a more compact form of writing a numerical value that represents a fractional value.
Earlier we learned about base-ten place value and how it is used to write whole number values. Now we extend the place-value concepts for the base-ten system to fractional parts of a whole.
In that earlier lesson, we noticed how each column in the place value system represents a value ten times greater than the value of the column immediately to the right. Since that time, we have studied exponents and now see that these place values are consecutive "powers of 10".
If we continue the patterns of each column being ten times the value of the column to the right, the next column to the right would have to be a value that when it is multiplied by 10 would equal the value of the last column, which is 1. This means the value of the next column to the right must be tenths, since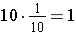 
. We abbreviate the common fraction 
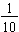by writing the decimal fraction 0.1; both values are read as "one-tenth". We call the first place-value after the decimal point the tenths position. Notice that the decimal place values end in -ths. Tens are whole values and tenths are fractional parts of the whole.
If we extend to the right one more column, that value would have to be the value that when we multiply it by ten it would equal one-tenth. That means the next column to the right would be the hundredths, since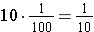 
. We abbreviate the common fraction 
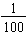as the decimal fraction 0.01. Again notice the "ths" ending. Hundreds are whole values and hundredths are fractional parts of the whole.
If we continue this process, we can extend the place value table out as far as we desire. As long as we have the table with the columns labeled, we can tell which column has which value. But when we write numbers without the table labels, we need to know where the place values change from whole numbers to fractions. That is the role of the decimal point. The decimal point separates the place values that are whole values on the left from the place values that are fractional parts on the right, as illustrated in the table below.
Note the thousandths position has a picture of the Missouri mill token; for more information on mill tokens used for taxes, see Mill (currency) - Wikipedia, the free encyclopedia.
It is interesting to note that if we continue the pattern of the exponents, the tenths' column corresponds to 10–1, the hundredths' column corresponds to 10–2, etc. This is consistent with the properties of exponents and operations with integers, which we will discuss further when we discuss integers. Note that the negative exponent could be interpreted as the reciprocal of the value, e.g., the reciprocal of 10 is 
or 10–1 is the reciprocal of 10 since 
. Another example, using the properties of exponents 
is the reciprocal of 100. Note that this is consistent with what we know the column values must be.
To write eight-tenths using decimal place value, the digit 8 is placed in the tenths' column. When we transfer the value out of the table, we need to include the decimal point. For better clarity and readability, when there are no whole number values, it is best to put a zero in front of the decimal point to indicate that there are no whole number values.
Note that we inserted a zero in the numeral where the table has an empty position since this simply says that position has no value. When we read decimal fractions (decimals) out loud or write them in words, the word and is placed where the decimal point occurs. In the table above, twenty and sixteen thousandths is an example of this.
Example: Write 127.836 in words, expanded fraction form, expanded decimal form and expanded exponential form.
|
words: |
one hundred twenty-seven and eight hundred thirty-six thousandths |
|
fraction expanded form: |
|
|
decimal expanded form: |
127.836 = 1 · 100 + 2 · 10 + 7 · 1 + 8 · 0.1 + 3 · 0.01 + 6 · 0.001 |
|
exponential expanded form: |
127.836 = 1 · 102 + 2 · 101 + 7 · 100 + 8 · 10–1 + 3 · 10–2 + 6 · 10–3
|
Note that 0.500 = 0.50 = 0.5, which follows from simplifying common fractions 
. The digit five remains in the tenths' column so these values are all equal to five-tenths. The extra zeros need not be written when writing decimals (decimal fractions) unless a person is working with problems where significant digits (Significant figures - Wikipedia, the free encyclopedia) need to be expressed, such has in scientific studies.
Write 305.0026 in words, expanded fraction from, expanded decimal form, and expanded exponential form.
|
words |
Solution |
|
fraction expanded form: |
Solution |
|
decimal expanded form: |
Solution |
|
exponential expanded form: |
Solution |
All common fractions can be written in decimal form. Some common fractions are easy to visualize as decimal fractions. For instance, we rewrite each of the common fractions, in the following examples, as a decimal by changing to an equivalent fraction that has denominator that is a power of ten. We use the fact that the prime factorization of each denominator has prime factors of 2 or 5, and the fact that the product of two and five is ten.
Examples: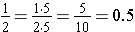 
or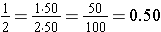 
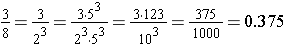
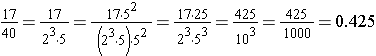
The above method works well when the denominator has only 2 or 5 as prime factors, but is there another method to convert common fractions? Another method to change a common fraction to a decimal fraction is to use the division interpretation of the fraction and continue the division on past the decimal point. In the example below, the division results in a terminating decimal. That means that it divides out completely, eventually having a remainder of zero.
|
Examples: |
To show |
To show |
To show |
|
|
|
|
|
What about common fractions where the denominator has a prime factor other than 2 or 5?
Write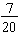 
as a decimal fraction.
Solution
Some common fractions, when we divide them out, never have a remainder of zero, instead the quotient forms a nonzero repeating pattern that never ends. The fraction 
is the most familiar of these type fractions that repeat in decimal form. If we divide 1 ÷ 3, we will get 0.333333 . . . and these threes will continue on forever, called a repeating decimal. The common notation we use to write these repeating decimals is to place a bar above the repeating digits, e.g., 
. The bar over the three means that the three repeats infinitely many times.
Important Note: Do not say or write 
. This is a false statement since 
but 
, an approximation not an equality. If the decimal is a repeating decimal, you must use either the ellipsis (…) or the repeat bar.
Most repeating decimals have several digits that repeat. For instance, 
.
Example: Express three-sevenths in decimal form.
Hence, we have 
.
Repeating decimal - Wikipedia, the free encyclopedia
Express five-sixths in decimal form.
Solution
Decimals that are not repeating decimals are called terminating decimals. Terminating decimals represent fractions that can be expressed with a denominator that is a power of 10. To change a terminating decimal to an equivalent common fraction, all we need to do is use place value to determine the denominator. Suggestion: Verbalize the decimal by reading it correctly, that is, read 0.025 as twenty-five thousandths.
Example:
Convert 0.35 and 0.175 to a simplified common fractions.
Solution for 0.35 --------------- Solution for 0.175
Repeating decimals can be changed to common fractions using an algebraic method. The method is to multiply the number by a power of ten that shifts the decimal point the number of place values that are repeating, and then subtract the number from that new value. This will cancel out the repeating portion.
Example: We change 
to a common fraction.
First we notice that multiplying by 10 moves the value one place value to the left in the place value table. For example, 7(10) =70 and this places the digit 7 one place value to the left of where it was in the original value of 7. Or, 0.77(10) = 7.7.
Let 
, then 
(just moving all the digits one place value to the left).
We then subtract these two values, and the repeating parts subtract completely off.
We solve this equation for x to obtain 
.
Example: We change 
to a common fraction.
First we notice that multiplying by 100 moves the two place values to the right, i.e., 
.
Let 
, then 
(just move all digits two place values to the left). We then subtract these two values, and the repeating parts subtract completely off.
We then solve this equation for x and simplify to obtain 
.
Example: We change 
to a common fraction.
Since there are only two positions repeating (the 32), we multiply by 100.
Let 
, then 
. The digits were all moved two place values to the left and the repeating part is still the 32.
After solving the equation and simplifying, we obtain 
.
Convert each repeating decimal to a simplified common fraction.
|
|
Solution |
|
|
Solution |
The polite mathematican says, "You go to infinity — and don't hurry back."
