and to the decimal fraction 0.17. We model 17% as the shaded area in a 10 × 10 grid in which 17 out of the 100 squares have been shaded. Reading and Writing Percents
Interpret each of the following statements.
A mortgage interest rate is 6.3%.
A CD earns 2.85%.
Many people tip 15%.
Each of the problems involves percentages, which are a very common method for stating ratios involving monetary values. The mortgage interest rate means that a person must pay $6.30 for every $100 borrowed, which is a ratio of 6.3 to 100. The CD earns $2.85 for every $100 put into the CD, which is a ratio of 2.85 to 100. A tip of 15% means that the people tip $15 for every $100 paid for a meal, which is a ratio of 15 to 100 or 3 to 20.
Remember, in our last lesson, we stated that a ratio is a comparison of the relative size of two numerical quantities. A percent is a special type of ratio where the second value is always 100.
Definition: A percent is ratio where n percent, denoted as n%, is the ratio n : 100. That is, a ratio compares numerical quantities in terms of the number of parts out of 100.
Note that the word percent is a statement of a ratio relationship and English "per cent" is derived from Latin "per centum" which means "per hundred". We use the root cent in many words in the English language.
Examples:
A century is 100 years.
Centigrade is the temperature scale where 0° is the freezing point and 100° is the boiling point of water.
A cent is a penny which is one hundredth of a dollar.
A centimeter 0.01 of a meter.
When we have 17 parts out of 100 (or part to whole ratio 17 : 100), we have 17%. The symbol % is called the percent sign. The expression 17% means 17 parts out of 100. Therefore, 17% is equivalent to the common fraction and to the decimal fraction 0.17. We model 17% as the shaded area in a 10 × 10 grid in which 17 out of the 100 squares have been shaded.
What percent of each figure is shaded?
First Grid Second Grid Third Grid
To change a percent into a common fraction, rewrite the percent as a ratio in fraction form, that is, 
and then simply the fraction.
Examples: Rewrite 70% and 200% as common fractions.
and 
.
Examples: Rewrite 31.5% and 0.3% as common fractions.
Again we use the definition of percent and write the ratio in fraction form, but note that the numerator contains a decimal in terms of tenths. To eliminate tenths and change the numerators to whole numbers, we use ten as a multiplier and then simplify the fractions.
Note that the values 
and 
in the examples above are not in the form of common fractions. We needed to multiply by 
to simplify each fraction since 31.5 and 0.3 are in tenths.
Examples: Rewrite 
and 
as common fractions.
Again we use the definition of percent and write the ratio in fraction form, but note that the numerator contains common fractions or mixed numbers. We use an appropriate multiplier and then simplify.
Note. Here are some basic percent-fraction equivalences that should be memorized for use with mental estimation.
Rewrite each percent as a common fraction.
|
2% |
Solution |
|
4.05% |
Solution |
|
|
Solution |
|
|
Solution |
To change percents into decimal form, we first interpret the percent as a ratio in fraction form as a part out of 100, and then change the fraction to a decimal by using place value.
Example: Rewrite 27% as a decimal.
which by decimal place value is 0.27.
Example: Rewrite 8% as a decimal.
which by decimal place value is 0.08.
Example: Rewrite 112% as a decimal.
112% can be changed to a decimal by first rewriting the fraction as a mixed number.
Example: Rewrite 4.5% as a decimal.
Note that in each example the decimal point is moved left two positions so that the ones position of the percent is placed in the hundredths position in the decimal form.
Convert each percent into a decimal.
|
40% |
Solution |
|
300% |
Solution |
|
3.8% |
Solution |
|
274% |
Solution |
First we use a place value table to illustrate the conversion of a decimal to a percent to show the movement of the decimal two positions to the right from after the ones position to after the hundredths position.
Also note that once we have a value written as a ratio in the fraction form "over 100", we convert directly to percent by the definition of percent. This is where the infamous "move the decimal point 2 places" rule comes from. What we are really doing is "reading the decimal value at the hundredths place value" as a way of getting a denominator of 100.
Values like 
and 
are not in the form of common fractions, since the numerator and denominator of a common fraction must be a whole number and 87.5 and 0.25 are not whole numbers. But these are arithmetic values that can be computed and they are exactly equal to the decimals 0.875 and 0.0025, respectively.
|
0.25 |
Solution |
|
0.182 |
Solution |
|
1.35 |
Solution |
|
41 |
Solution |
There are two common ways to translate a fraction into a percent:
(1) convert to an equivalent fractions with a denominator of 100, or
(2) use the division interpretation of the fraction.
Fractions that have denominators that are factors of 100 can be rewritten with a denominator of 100 and are easy to translate into percents by using the definition of percent. All we need to do is to convert to the equivalent fraction that has 100 as a denominator.
Examples: Convert seven hundredths, one-half, and one-fourth to percents.
, 
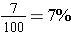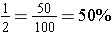, and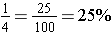 
This works well for fractions that are easy to convert to fractions with denominators of 100, but the division interpretation of fractions would probably work better for most fractions.
Fractions that have denominators that are not factors of 100 are best converted to their decimal form before finding the equivalent percent. When the decimal equivalent is a terminating decimal, we can find the percent by "reading it off at the hundredths place".
Example: Convert one-eighth to a percent.
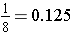
How many hundredths is this?
Since the hundredths place value is the second decimal place behind the decimal point, we read 0.125 as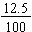 
which in turn can be written as 12.5%. This is where the infamous "move the decimal point 2 places" rule comes from. What we are really doing is reading the decimal value at the hundredths place value.
As we have seen before, many fractions do not terminate. For example, the fraction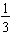 
has a repeating decimal form 
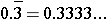. The exact percent equivalent for 
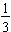is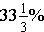 
. We see this by looking at 
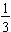and how it is divided into a decimal form where we write the remainder of the hundredths position as a fraction.
We usually do not write percents as repeating decimals. We either write them with a fractional part of a percent or we round it to a certain decimal position. This rounding is what causes the common misconception that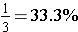 
or just 33%. The common fraction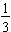 
is approximately equal to 33.3% written as 
.
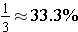The fraction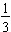 
is exactly equal to 
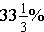. In this class, unless otherwise stated give the exact amount; you must give the percent that is exactly equal to the amount given.
When working application problems, approximations may be used, but be sure that you use a symbol that states that your answer is an approximation. Use either the symbol ≈ or 
for "approximately equal to". Your instructor will tell you which symbol the instructor wants you to use.
For more discussion on approximations and rounding see Session 28.
Convert each fraction to a percent.
|
|
Solution |
|
|
Solution |
|
|
Solution |
|
|
Solution |
A parent was complaining to the stock broker. "I have spent nearly $20,000 on my child's education. And here Dana goes and marries someone with an income of only $1400 a year."
"Well," replied the broker, "that's a seven percent return on your investment. What more can you expect in these times?"
