Percent Off, Increase, Decrease
Consider the following problem involving stock prices.
In recent years, the stock market has been quite volatile. Suppose your stock investment was initially $100,000. After a period where the value first decreased by 20% and then the value increased by 20%, would the value still be $100,000?
Many people, including some financial advisors, would answer the question in the affirmative; they would say your stock would still be valued at $100,000. But let's compute the result before we answer the question. Since the stock first decreased by 20%, we take 20% of $100,000, which is $20,000. So, the value of the stock would then be $80,000. The 20% increase would be on the $80,000. Taking 20% of $80,000, we obtain $16,000, which means the stock increases in value by $16,000. Therefore, the stocks final value is $96,000. The answer to the question is no since the value has had a net decrease of $4,000.
This answer seems counterintuitive since we had a 20% decrease and a 20% decrease. But note that the 20% decrease was on a greater value than the 20% increase. The changes were not on the same stock values.
What would be the result if the reverse happened, that is, first have a 20% increase followed by a 20% decrease?
The 20% increase on $100,000 would be an increase of $20,000. So, the new value would be $120,000. We find the 20% of $120,000 is $24,000. Therefore, we would have a decrease of $24,000 for a net value of $96,000. Note that we have obtained the same result. The order of the increase and decrease did not matter, again because the 20% decrease was taken on the greater value than the 20% increase.
The Commutative Property of Multiplication may be used to show that the above two problems will have the same result. First note that 100% of $100,000 is $100,000. A decrease of 20% of the value would mean that the final value would be 80% of the original value since 100% – 20% = 80%. Also, an increase of 20% of the value would mean that the final value would be 120% of the original value since 100% + 20% = 120%. Reword the problems: Find 120% of 80% of $100,000 or find 80% of 120% of $100,000. Translate the problems:
1.20(0.80)(100,000) = 0.80(1.20)(100,000).
The commutative property shows that the two problems are equivalent. Multiplying either side of the equation we obtain our solution of $96,000.
Further note that $96,000 is a 4% decrease from the original $100,000 since we had a decrease of $4,000.
The above problem is a illustration of a common type of problem involving percentages where percents are used to describe how prices, salaries, and other monetary situations change. For instance, the TV you want to buy is on sale for 30% off or you get a 3.5% increase in your salary starting July 1.
Knowing what these phrases mean and knowing how to compute the values is important to everyone in our society.
We frequently face situations in which items are on sale and the sale price is described as x% off. This type of problem may be solved as either a two step or a one step computation.
Example: We desire to buy a TV that has a list price of $600, but is on sale for 30% off.
Two steps: First we compute 30% of 600 which tells us how much we will save by buying the TV on sale.
0.30($600) = $180. This is the amount saved.
Then the amount we actually pay (before tax) would be $600 – $180 = $420. The sale price of the TV is $420.
In order to solve the problem in one step, we note that the list price is 100% of the list price and the list price is being reduced by 30% of the list price. Therefore, we would pay 70% of the list price, since (100% – 30%) = 70%. So if all we are interested in is the sale price of the TV, we can compute 70% of $600.
One step: 70% of $600 which is 0.7($600) = $420.
The sale price of the TV is $420.
A MD Hardware is holding a "Bag Sale" where a person will get 40% off on the price of all items that the person puts in the bag. The total value of all items in Pat's bag is $397. How much does Pat have to pay?
Solution
Reduced by 20%, Decreased by 20%, and Received a 20% Discount all mean the same as 20% off. In any of these cases, we still have a choice of working the problem in one step or in two steps.
Example: In order for everyone at the company to keep their jobs during the recession, each person's salary is reduced by 20%. To figure out what a salary would be after this pay cut, we would find 20% of the current salary, and then subtract the result from the current salary. Or we could also just compute 80% of the current salary, since 100% – 20% = 80%.
Two steps: For a current salary of $30,000 that is to be reduced by 20%, we find the amount of pay cut by finding the amount the salary is reduced by and then subtracting the result from the current salary.
The amount being cut is 20% of $30,000, which is 0.2($30,000) = $6,000.
So the reduced salary is $30,000 – $6,000 = $24,000.
One step: We may also find the reduced salary in a single step. Since 100% – 20% = 80%, this means that your reduced salary will be 80% of your current salary.
So your reduced salary is 80% of $30,000, which is 0.8($30,000) = $24,000.
A DevMart has advertised that the price of all items in the store are being reduced by 15%. Lynn has a DevMart coupon for a 10% discount on on any item purchased. If Lynn is allowed to have both the price reduction and to use the coupon, what percent decrease in price would Lynn get on any purchased item?
Solution
Increased by is similar to decreased by in that we have a choice of solving the problem in two steps or just one step. The difference is that with increased by we are beginning with the whole amount (100%) and then increasing that amount by an additional amount. This means that instead of subtracting we add the amount indicated by the percentage.
Example: What is your new salary if your current salary of $24,000 is increased by 3.5%?
Two steps: Find 3.5% of $24,000.
0.035($24,000) = $840.
Then old salary + increase = new salary.
$24,000 + $840 = $24,840.
The new salary is $24,840.
Your new salary is 100% of your current salary plus 3.5% of your current salary. This means that your new salary is (100% + 3.5%) = 103.5% of your current salary. So we work the problem in one step by finding 103.5% of your current salary.
One step: Find 103.5% of 24,000.
1.035($24,000) = $24,840.
The new salary is $24,840.
Notice in the example above that to solve the increased by problem in one step, we work with a percent that is greater than 100%. This makes sense because we are getting 100% of our current salary PLUS the increase.
Sam owns stock in MDV. Sam heard on the news that a share of MDV stock increased by 4.2% today but missed hearing today's price. Sam remembers that the closing price yesterday was 83.5. What was today's closing price?
Solution
Frequently, we know the new amount and the percent change and need to know the original amount. We reconsider the television problem from the beginning of the lesson. We found that a $600 TV on sale for 30% off, cost $420 on sale. We might think, that to find the original cost of the TV that has a sale price of $420 after a sale of 30% off, we could just take 30% of the $420 cost and add it back to the $420 to find the original cost. NOTE THAT THIS DOES NOT WORK:
30% of $420 is 0.30($420) = $126 and $420 + $126 = $546.
Or, 130% of $420 is 1.3($420) = $546.
Notice that this is not the $600 original list price with which we started.
Why doesn't this work?
The method does not work because 30% of $420 is not the same amount as the 30% of $600. It may seem obvious when stated this way, but it is a very common error made on problems of this type. We cannot just use the same percent and get back to the original amount because we are taking that percent of a different value.
To work problems of this type correctly, it is generally best to write an equation for the situation and then solve.
Example: Since (100% – 30%)(original price) = (sale price)
70% of the (original price) is $420.
0.7x = 420
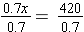
x = 600
The original cost was $600.
We may also solve this problem using the two-step method. Working the problem in two steps requires us to use more algebra skills. We have to know that x = 1x (Identity Property of Multiplication) and that 1x – 0.3x = 0.7x (subtracting like terms). Then we solve the problem as follows:
(original price) – 30%(original price) = sale price
x – 0.3x = 420
0.7x = $420
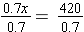
x = 600
The original cost was $600.
Note that with both of the above methods we do obtain the correct original amount.
Example: After a 5% pay raise, Hermione is earning $22,680 per year. What was she earning before the pay raise?
105% of (original salary) = current salary
1.05x = 22,680

x = 21,600
Hermione earned $21,600 per year before the pay raise.
A VEDM, Inc. states that it make as 30% profit over its expenses for producing its new product the hMat. VEDM, Inc. sells each hMat for $377. How much does it cost VEDM, Inc. to make each hMat?
Solution
Three traffic engineers were boasting about improvements in their respective city traffic flows, which improved 911 emergency vehicle response times.
First Engineer: "Since we installed our new satellite navigation system, we've cut our emergency response time by ten percent."
Second Engineer: "Not bad,but by using a computer model of traffic patterns, we we cut our average time by 20 percent."
Third Engineer: "That's nothing, since our city manager passed the bar exam, we've cut our emergency response time in half!"