Five-Number Summary and Box-and-Whisker Plots
Motivation Problem
Interpret the information given in the following box-and-whisker plot.
The results from a pre-test for students for the year 2000 and the year 2010 are illustrated in the box plot. What do these results tell us about how students performed on the 29 question pre-test for the two years? 
If we compare only the lowest and highest scores between the two years, we might conclude that the students in 2010 did better than the students in 2010. This conclusion seems to follow since the lowest score of 8 in 2010 is greater in value than the lowest score of 6 in 2000. Also, the highest score of 28 in 2010 is greater in value than the highest score of 27 in 2000.
But the box portion of the illustration gives us more detailed information. The middle bar in each box shows us that the median score of 20 in 2000 is greater in value than the median score of 17 in 2010. Further, we note that the box and whiskers divide the illustration into four pieces. Each of these four pieces represents the same portion of students. So, the upper half of the students in 2000 scored in the same score range as the upper one-fourth of the students in 2010, see the illustration at a score of 20.
By considering the upper one-fourth, upper half, and upper three-fourths instead of just the lowest and highest scores, we would conclude that the students as a whole did much better in 2000 than in 2010. We would conclude that as a whole the students in 2010 are less prepared than the students in 2000.
In this section, we discuss box-and-whisker plots and the five key values used in constructing a box-and-whisker plot. The key values are called a five-number summary, which consists of the minimum, first quartile, median, third quartile, and maximum.
Brief Review of Median
In previous sessions, we worked problems involving the mean and median. For this session, we primarily use the median. Here is a brief review of terms used with the median:
- A data set is any finite set of real numbers.
- A data set is in increasing order if the numbers in the data set are arranged from the least value to greatest value with the least value on the left and the greatest value on the right.
- The median of a data set is the number that, when the set is put into increasing order, divides the data into two equal parts.
- If a data set has an odd number of data points, then the median is the middle data value (when the data is in increasing order).
- If a data set has an even number of data points, then the median is the mean of the two middle data values (when the data is in increasing order).
Example 1: Find the median of the data set {3, 7, 8, 5, 12, 14, 21, 13, 18}.
First, we put the values in the data set into increasing order: 3, 5, 7, 8, 12, 13, 14, 18, 21. Notice that the number of data values is 9, which is odd (there are nine numbers in this data set). Then the middle data value is the 5th value, counting from either the left or the right. Therefore the median is 12.
(The values 3, 5, 7, and 8 are to the left of 12, and 13, 14, 18, and 21 are to the right of 12.)
Example 2: Find the median of the data set {3, 7, 8, 5, 12, 14, 21, 15, 18, 14}.
Note that here we consider the two 14's to be distinct elements and not representing the same item; consider this like you obtained a score of 14 on two different quizzes.
First, we put the values into increasing order: 3, 5, 7, 8, 12, 14, 14, 15, 18, 21. Notice that there are 10 values, which is even. Then the middle data values are the 5th value from the left and the 5th value from the right. That is, 12 and 14 (the leftmost of the two 14s). Therefore the median is the mean of the two middle values: The median is 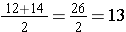 .
.
Self Check Problem
The following dollar amounts were the hourly collections from a Salvation Army kettle at a local store one day in December: $19, $26, $25, $37, $32, $28, $22, $23, $29, $34, $39, and $31. Determine the median amount collected.
Solution
First Quartile and Third Quartile
Definitions:
- The lower half of a data set is the set of all values that are to the left of the median value when the data has been put into increasing order.
- The upper half of a data set is the set of all values that are to the right of the median value when the data has been put into increasing order.
- The first quartile, denoted by Q1 , is the median of the lower half of the data set. This means that about 25% of the numbers in the data set lie below Q1 and about 75% lie above Q1 .
- The third quartile, denoted by Q3 , is the median of the upper half of the data set. This means that about 75% of the numbers in the data set lie below Q3 and about 25% lie above Q3 .
Example 1: Find the first and third quartiles of the data set {3, 7, 8, 5, 12, 14, 21, 13, 18}.
First, we write data in increasing order: 3, 5, 7, 8, 12, 13, 14, 18, 21.

As on the previous page, the median is 12.
Therefore, the lower half of the data is: {3, 5, 7, 8}.
The first quartile, Q1, is the median of {3, 5, 7, 8}.
Since there is an even number of values, we need the mean of the middle two values to find the first quartile:
 .
.
Similarly, the upper half of the data is: {13, 14, 18, 21}, so
 .
.
Example 2: Find the first and third quartiles of the set {3, 7, 8, 5, 12, 14, 21, 15, 18, 14}.
Note that here we consider the two 14's to be distinct elements and not representing the same item; consider this like you obtained a score of 14 on two different quizzes.
First, we write the data in increasing order: 3, 5, 7, 8, 12, 14, 14, 15, 18, 21.
As before, the median is 13 (it is the mean of 12 and 14 — the pair of middle entries).
Therefore, the lower half of the data is: {3, 5, 7, 8, 12}.
Notice that 12 is included in the lower half since it is below the median value.
Then Q1 = 7 (there are five values in the lower half, so the middle value is the median). Similarly, the upper half of the data is: {14, 14, 15, 18, 21}, so Q3 = 15.
Self Check Problem
The following dollar amounts were the hourly collections from a Salvation Army kettle at a local store one day in December: $19, $26, $25, $37, $32, $28, $22, $23, $29, $34, $39, and $31. Determine the first quartile and third quartile for the amount collected.
Solution
Five-Number Summary
Definitions:
- The minimum value of a data set is the least value in the set.
- The maximum value of a data set is the greatest value in the set.
- The range of a data set is the distance between the maximum and minimum value. To compute the range of a data set, we subtract the minimum from the maximum:
range = maximum – minimum.
- The interquartile range of a data set is the distance between the two quartiles.
Interquartile range = Q3 – Q1.
Example 1: Find the range and interquartile range of the set {3, 7, 8, 5, 12, 14, 21, 13, 18}.
First, we write the data in increasing order: 3, 5, 7, 8, 12, 13, 14, 18, 21.
range = max – min = 21 – 3 = 18.
Recall from the previous page that Q1 = 6 and Q3 = 16.
Therefore, the interquartile range = Q3 – Q1 = 16 – 6 = 10.
The range is 18 and the interquartile range is 10.
Example 2: Find the range and interquartile range of the set {3, 7, 8, 5, 12, 14, 21, 15, 18, 14}.
First, we write the data in increasing order: 3, 5, 7, 8, 12, 14, 14, 15, 18, 21.
range = max – min = 21 – 3 = 18.
Recall from the previous page that Q1 = 7 and Q3 = 15.
Therefore, the interquartile range = Q3 – Q1 = 15 – 7 = 8.
The range is 18 and the interquartile range is 8.
Self Check Problem
The following dollar amounts were the hourly collections from a Salvation Army kettle at a local store one day in December: $19, $26, $25, $37, $32, $28, $22, $23, $29, $34, $39, and $31. Determine the range and interquartile range for the amount collected.
Solution
Definition: The five-number summary of a data set consists of the five numbers determined by computing the minimum, Q1 , median, Q3 , and maximum of the data set.
Example 1: Find the five-number summary for the data set {3, 7, 8, 5, 12, 14, 21, 13, 18}.
From our Example 1's on the previous pages, we see that the five-number summary is:
Minimum: 3 Q1 : 6 Median: 12 Q3 : 16 Maximum: 21
Example 2: Find the five-number summary for the data set {3, 7, 8, 5, 12, 14, 21, 15, 18, 14}.
From our Example 2's on the previous pages, we see that the five-number summary is:
Minimum: 3 Q1 : 7 Median: 13 Q3 : 15 Maximum: 21
Self Check Problem
The following dollar amounts were the hourly collections from a Salvation Army kettle at a local store one day in December: $19, $26, $25, $37, $32, $28, $22, $23, $29, $34, $39, and $31. Find the five-number summary for the amount collected.
Solution
Box-and-Whisker Plot
Definition: A box-and-whisker plot or boxplot is a diagram based on the five-number summary of a data set.
To construct this diagram, we first draw an equal interval scale on which to make our box plot. Do not just draw a boxplot shape and label points with the numbers from the 5-number summary. The boxplot is a visual representation of the distribution of the data. Greater distances in the diagram should correspond to greater distances between numeric values.
Using the equal interval scale, we draw a rectangular box with one end at Q1 and the other end at Q3. And then we draw a vertical segment at the median value. Finally, we draw two horizontal segments on each side of the box, one down to the minimum value and one up to the maximum value, (these segments are called the "whiskers").
Example 1: Draw a box-and-whisker plot for the data set {3, 7, 8, 5, 12, 14, 21, 13, 18}.
From our Example 1 on the previous page, we had the five-number summary:
Minimum: 3, Q1 : 6, Median: 12, Q3 : 16, and Maximum: 21.

Notice that in any box-and-whisker plot, the left-side whisker represents where we find approximately the lowest 25% of the data and the right-side whisker represents where we find approximately the highest 25% of the data. The box part represents the interquartile range and represents approximately the middle 50% of all the data. The data is divided into four regions, which each represent approximately 25% of the data. This gives us a nice visual representation of how the data is spread out across the range.
Example 2: Draw a box-and-whisker plot for the data set {3, 7, 8, 5, 12, 14, 21, 15, 18, 14}.
From our Example 2 on the previous page, we had the five-number summary:
Minimum: 3, Q1: 7, Median: 13, Q3: 15, and Maximum: 21.

When we relate two data sets based on the same scale, we may examine box-and-whisker plots to get an idea of how the two data sets compare.
Example 3: Suppose that the box-and-whisker plots below represent quiz scores out of 25 points for Quiz 1 and Quiz 2 for the same class.
What do these box-and-whisker plots show about how the class did on test #2 compared to test #1?

These box-and-whisker plots show that the lowest score, highest score, and Q3 are all the same for both exams, so performance on the two exams were quite similar. However, the movement Q1 up from a score of 6 to a score of 9 indicates that there was an overall improvement. On the first test, approximately 75% of the students scored at or above a score of 6. On the second test, the same number of students (75%) scored at or above a score of 9.
Self Check Problem
The following dollar amounts were the hourly collections from a Salvation Army kettle at a local store one day in December: $19, $26, $25, $37, $32, $28, $22, $23, $29, $34, $39, and $31. Construct the box-and-whisker plot for the amount collected.
Solution
Joke or Quote
He uses statistics as a drunken man uses lamp posts — for support rather than illumination.
Andrew Lang (1844-1912)
Treasury of Humerous Quotations
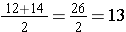 .
.  .
. .
.