Solution to Exercise 2.57.
The value of Euclid's work as a masterpiece of logic has been grossly exaggerated.
—Bertrand Russell (1872–1970)

Exercise 2.57. Prove Theorem 2.12. Given a line and a point not on the line, there exists a unique line perpendicular to the given line through the given point.

 

Proof. Let l be a line and P be a point not on line l.  Let A and B be two points on line l. By the Angle Construction Postulate, there is a ray AQ with Q and P on opposites sides of line l and  By the Ruler Postulate, there is a point R on line AQ and on the same side of line l as Q such that AR = AP. Note that P and R are on opposite sides of line l. Hence, by the Plane Separation Postulate, there is a point C on line l such that P-C-R. One of the following is true: A-B-C, C = B, A-C-B, C = A, or C-A-B.

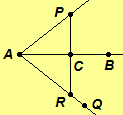
       Case 1. Assume A-B-C, C = B, or A-C-B. Since   and  we have  Hence,  Thus  and  are a linear pair of congruent angles, since P-C-R. Since a linear pair of congruent angles are right angles, line PR is perpendicular to line  

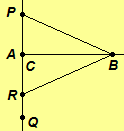
       Case 2. Assume C = A. Since  and P-A-R,  and  are a linear pair of congruent angles. Since a linear pair of congruent angles are right angles, line PR is perpendicular to line  

       Case 3. Assume C-A-B. Then  and  are a linear pair. Also,  and  are a linear pair. Hence, by the Supplement Postulate and 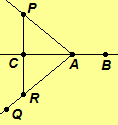the definition of supplementary angles,  and  Therefore,

 

Since   and  we have  Hence,  Thus  and  are a linear pair of congruent angles, since P-C-R. Since a linear pair of congruent angles are right angles, line PR is perpendicular to line  

       All cases show that there exists a line through P perpendicular to line l. We need to show that the line is unique. Suppose there are two lines through P that are perpendicular to line l. Let A and B be the points on line l where the two perpendicular lines intersect line l. Let C be a point on line l such that A-B-C. Then  is an exterior angle of . By the Exterior Angle Theorem,  Since line PB and line PA are perpendicular to line l,  and  are right angles. Thus,  But, this is a contradiction. Therefore, the line through P that is perpendicular to line l is unique.//