Exercises

Exercises for Chapter Four Printout
We don't know all the answers. If we knew all the answers we'd be bored, wouldn't we? We keep looking, searching, trying to get more knowledge.

—Jack LaLanne (1914–2011)

Exercise 4.1. Write the proof for Theorem 4.1.

Exercise 4.2. Prove Theorem 4.2. (Caution: You may not assume the existence of any points or any lines.)

Exercise 4.3. Prove Theorem 4.3. (Caution: You may not assume a line has any points.)

Exercise 4.4. Prove Theorem 4.4. (Hint: You may need to use Axiom 4.)

Exercise 4.5. Prove the existence of a complete quadrangle.

Exercise 4.6. Is it possible to extend Theorems 4.3 and 4.4 to an arbitrary number of points? Explain.

Exercise 4.7. Consider just the first three axioms. Show they are independent. (Similar to problems in Chapter One. Examples of Axiomatic Systems.)

Exercise 4.8. Show Axiom 4 is independent of Axioms 1–3. (Hint. Consider the projective plane of order 2 in Chapter One. A Finite Plane Projective Geometry.)

Challenge Exercise 4.9. Show Axiom 5 (Desargues' Theorem) is independent of Axioms 1–4.

Challenge Exercise 4.10. Show Axiom 6 is independent of Axioms 1–5.

Exercise 4.11. Write the dual and proof for Axiom 2.

Exercise 4.12.
        (a) How many cases are there in the proof of the Dual of Axiom 3?
        (b) State the other cases.
        (c) Prove at least one of the cases.

Exercise 4.13.
        (a) Prove the existence of a complete quadrilateral.
        (b) What are similarities and differences between complete quadrilaterals and complete quadrangles.
        (c) What are similarities and differences between complete quadrilaterals and Euclidean quadrilaterals.

Exercise 4.14.
(a) Prove that every point is incident with at least three distinct lines.
(b) Prove that every point is incident with at least four distinct lines.

Exercise 4.15. Prove the Dual of Axiom 6.

Exercise 4.16. Construct two triangles that are perspective from a point, then determine the line from which the triangles are perspective. (You may use dynamic geometry software.)

Exercise 4.17. Construct two triangles that are perspective from a line, then determine the point from which the triangles are perspective. (You may use dynamic geometry software.)

Exercise 4.18. Use dynamic geometry software for this exercise. In the Poincaré Half-plane, construct two triangles that are perspective from a point. Investigate whether the triangles are also perspective from a line.

Exercise 4.19. Given ΔABC and ΔDEF. Assume D is on BC, E is on AC, and F is on AB such that AD, BE, and CF are concurrent. Show that if AB ·DE = P, AC ·DF = Q, and BC ·EF = R, then P, Q, and R are collinear.

Exercise 4.20. Prove that D is distinct from A, B, and C.

Exercise 4.21. Consider the dual of a harmonic set of points.

Write the definition for the dual of a harmonic set of points.
Write the dual for each of the four theorems.
Prove the theorems stated in part (b). (Hint. Use the principle of duality.)

Exercise 4.22. Write the proof for Theorem 4.5, the existence of a harmonic set of points that was briefly described in this section.

Exercise 4.23. Construct each of the following where the points or lines are located as in each illustration. (You may use dynamic geometry software.)

Construct the harmonic conjugate of C with respect to A and B.
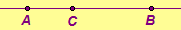
Construct the harmonic conjugate of C with respect to A and B.
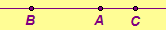
Construct the harmonic conjugate of c with respect to a and b.
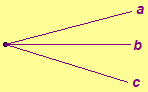
Construct the harmonic conjugate of c with respect to a and b.

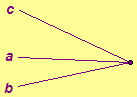
Exercise 4.24. Let M be the midpoint of a Euclidean segment AB. Determine, if possible, the harmonic conjugate of M with respect to A and B. (Hint. Use dynamic geometry software to help investigate.)

You may use dynamic geometry software for each of the following exercises.

Exercise 4.25. The frequency ratio 3:4:5 is equivalent to the ratio 1:4/3:5/3, which gives the chord F, A, C called the subdominant of the major triad of the example above. As with the example, show H(OF, CA) where OF is 3/4 of the length of OC and OA is 3/5 of the length of OC.

Exercise 4.26. The frequency ratio 3:4:5 is also equivalent to the ratio 3/2:15/8:9/8, which gives the chord G, B, D called the dominant of the major triad of the example above. As with the example, show H(OG, DB) where OG = (2/3)OC, OB = (8/15)OC, and OD = (8/9)OC.

Exercise 4.27. A different scale called the equal temperament scale is used in tuning pianos. The frequency ratios are 1.000 (C) : 1.122 (D) : 1.260 (E) : 1.335 (F) : 1.498 (G) : 1.682 (A) : 1.888 (B). If a string is tuned to C (as with the example above) and the equal temperament scale is used, investigate whether or not the major triad C, E, and G determines a harmonic set H(OE, CG)

Exercise 4.28. Symbolize each perspectivity forming the projectivity in each of the above diagrams.

Exercise 4.29. Find the image of the point D or line d for each projectivity.

Exercise 4.30. Show that P in the constructive proof of Theorem 4.10 exists.

Exercise 4.31. (a) State and prove the dual of Theorem 4.10. (Hint: principle of duality) (b) Assume a, b, c are elements of a pencil with center P and a', b', c' are elements of a pencil with center P'. Use dynamic geometry software to construct and find a corresponding line d' of a line d. (Hint: write the dual of the steps of the construction for points.)

Exercise 4.32. Given four collinear points A,B,C,D, use a dynamic geometry software to construct each projectivity and the image of the fourth point.

Exercise 4.33. Given four concurrent lines a,b,c,d, use a dynamic geometry software to construct each projectivity and the image of the fourth point.

Exercise 4.34. Given three concurrent lines a, b, and c and two points P and Q not on any of the three lines. If A_i, and B_i are points on a and b, respectively, such that A_iP · B_iQ = C_i is on line c, then .

Exercise 4.35. Prove Corollary 4.12. (Remember a perspectivity is a projectivity, but a projectivity need not be a perspectivity.)

Exercise 4.36. Show the complete quadrilateral defined by FG, FH, AH, and AB in the above proof is in fact a complete quadrilateral.

Exercise 4.37. Prove Theorem 4.14.

Exercise 4.38. Investigation for an Alternate Construction of a Projectivity. The construction of the proof of Theorem 10 requires several steps to construct a projectivity between two pencils of three points. Another method is often used that is more efficient. In the given diagram, the two pencils of points are projectively related, Draw the lines and points AB' · BA', AC' · CA', AD' · DA', BC' · CB', BD' · DB', and CD' · DC'. (The pairs of lines, you drew, are called cross joins.)

(a) How are the points related to each other? (b) State your result as a conjecture. (c) Now let E be an arbitrary point on the pencil of points with A, B, C, D. Based on your conjecture of the projectivity, construct the image of E.

Exercise 4.39. Construct the axis of homology for two projectively related pencils of points. Then use the construction to determine an image of an arbitrary point. (May use dynamic geometry software.)

Exercise 4.40. Construct the center of homology for two projectively related pencils of lines. Then use the construction to determine an image of an arbitrary line. (May use dynamic geometry software.)

Exercise 4.41. Construct the projectivity as a product of two perspectivities determined by a point conic formed from five points, no three collinear. Use the projectivity to construct a sixth point of the point conic. (May use dynamic geometry software.)

Exercise 4.42. Construct the projectivity by using the center of homology determined by a point conic formed from five points, no three collinear. Use the projectivity to construct a sixth point of the point conic. (May use dynamic geometry software.)

Exercise 4.43. (a) State the dual of Exercise 4.41 and perform the construction. (b) State the dual of Exercise 4.42 and perform the construction. (May use dynamic geometry software.)

Exercise 4.44. Prove that any three distinct points in a point conic are noncollinear.

Exercise 4.45. The definition of point conic includes the phrase "but not perspectively." If this phrase is omitted from the definition, the result would allow all of the points on two lines as points of the point conic. What two lines, defined by the perspectivity, would they be?

Exercise 4.46. (a) How many ways may the simple hexagon ABCDEF be named? (b) How many distinct simple hexagons are determined by six distinct points?

Exercise 4.47. (a) How many cases are there in the proof of Theorem 4.19? (b) Extend the proof to include the case where A and C are the centers.

Exercise 4.48. Prove Pascal's Theorem.

Exercise 4.49. Use Pascal's Theorem to construct a sixth point in a point conic formed from five points, no three collinear. (May use dynamic geometry software.)

Exercise 4.50. Use Brianchon's Theorem to construct a sixth line in a line conic formed from five lines, no three concurrent. (May use dynamic geometry software.)

Exercise 4.51. Complete the case where F = C in the proof of Theorem 4.24.

Exercise 4.52. Given five points of a point conic, construct the tangent to one of the points by construction of the projectivity as in the proof of Theorem 4.22. (May use dynamic geometry software.)

Exercise 4.53. Given five points of a point conic, construct the tangent to one of the points applying Theorem 4.24 (the degenerate form of Pascal's Theorem.) (May use dynamic geometry software.)

Exercise 4.54. Prove Theorem 4.25.