Psy 230
Stats/Methods I
Intro to
Statistics
Chapter 1 (G&W)
Variables
A
variable is a characteristic or
condition that can change or take on different values.
Most research begins with a general question about the
relationship between two variables for a specific group of
individuals.
Populations and Samples
The entire group of
individuals is called the
population.
For example, a researcher may be interested in the relation
between class size (variable 1) and academic performance
(variable 2) for the population of third-grade children.
Usually populations are so
large that a researcher cannot examine the entire group.
Therefore, a
sample is selected to represent
the population in a research study. The goal is to use the
results obtained from the sample to help answer questions about
the population.
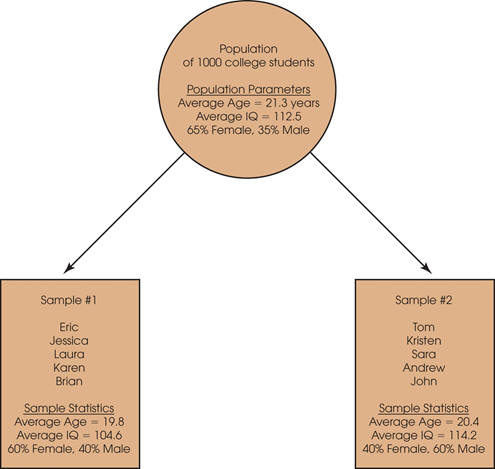
Parameters and Statistics
Descriptive statistics
are methods for organizing
and summarizing data.
When describing data with
descriptive statistics, it is
necessary to distinguish whether the data come from a population or a sample.
Typically, every population
parameter has a corresponding sample statistic.
-
Parameter—a descriptive value that describes a population
-
Statistic—a descriptive value that describes a sample
Descriptive Statistics vs.
Inferential Statistics
Descriptive Stats
techniques
used to summarize, organize, and simplify data
can't look at it all - get a quick, good impression
Inferential Stats
techniques used to study samples and then make generalizations
about the populations from which they were selected. Use sample statistics
to make inferences about the corresponding population parameters.
A
drawback?
Sampling Error
The discrepancy between a sample statistic and its population
parameter is called
sampling error.
Defining and measuring sampling error is a large part of
inferential statistics.
Variables
discrete - separate categories.
No values can exist between two neighboring categories (e.g., dice)
continuous - infinite fineness.
There are an infinite number of possible values that fall between any two
observed values
•For
example, time can be measured to the nearest minute, second,
half-second, etc.
-
each score corresponds to an interval of the scale
-
the boundaries that separate these intervals are called real
limits
Measuring Variables
To establish relationships between variables,
researchers must observe the variables and
record their observations.
This requires that the variables be
measured.
Scales of Measurement
The
process of measuring a variable requires a set of categories called a scale of
measurement and a process that classifies each individual into one category.
Four Types of Measurement Scales:
Nominal - discrete categories
The
categories represent qualitative differences in the variable being measured.
Can only determine same or different
Ordinal - ordering or ranking
Often
consists of a series of ranks or verbal labels
The
categories form an ordered sequence
Can determine direction of difference between two individuals
Interval - how far apart on a given dimension
Categories
are ordered sequentially, and all categories are the same size
Can determine direction AND magnitude of a difference
Arbitrary
zero point---zero does NOT mean a complete absence of the attribute being
measured (e.g., °F, IQ)
Ratio - an interval scale with an absolute zero point
Equal, ordered
categories and the value 0 means a complete absence of
the variable being measured (e.g., height in inches, weight in lbs.)
Can determine direction and magnitude of a
difference and ratio comparisons make sense
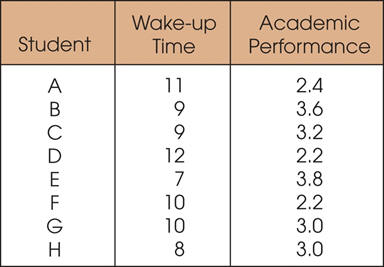
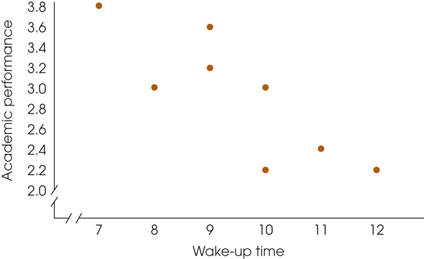
Correlational Studies
The goal of a
correlational study is to determine
whether there is a relationship between two variables and to
describe the relationship.
Correlation coefficient quantifies degree and direction of
relationship
A
correlational study simply observes the
two variables as they exist naturally.
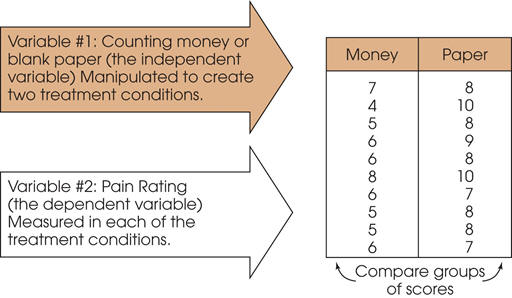
Experiments
The goal of an
experiment is to demonstrate a
cause-and-effect relationship between two variables; that is, to
show that changing the value of one variable causes changes to
occur in a second variable.
In an
experiment, one variable is
manipulated to create treatment conditions.
A second variable is observed and measured to obtain
scores for a group of individuals in each of the treatment
conditions.
–The
measurements are then compared to see if there are differences
between treatment conditions.
All other variables are controlled to prevent them from
influencing the results.
–The
manipulated variable is called the independent variable and the
observed variable is the dependent variable.
4
characteristics of true experiments:
1
– MANIPULATION
2
– MEASUREMENT
3
–COMPARISON
4
– CONTROL
Try this exercise
Difference between an experiment and quasi-experiment?
Quasi-experiments aim to establish a tentative cause and effect
relationship between two variables but cannot satisfy all of the strict
requirements needed for a true experiment (often cannot not meet all of the
above requirements in a natural settings). Introduce some treatment or
manipulation.
Uses some of the rigor and control
used in true experiments. But in some way, lack the control found in true
experiments (usually lack random assignment of participants to conditions), so ability to draw a causal inference is impaired
See
G&W Appendix A for a math review--I'm assuming you possess these basic
skills...If not, you need to develop them before taking this class.
You
must know and be VERY comfortable with the order of operations!!
P E M D A S
Order of Operations
1.All calculations within parentheses are done first.
2.Squaring or raising to other exponents is done second.
3.Multiplying, and dividing are done third, and should be
completed in order from left to right.
4.Summation with the Σ notation is done next.
5.Any additional adding and subtracting is done last and should
be completed in order from left to right.
Statistical Notation
•The individual measurements or scores
obtained for a research participant will be
identified by the letter X (or X and Y if there
are multiple scores for each individual).
•The number of scores in a data set will
be identified by N for a population or n for a
sample.
•Summing a set of values is a common
operation in statistics and has its own
notation. The Greek letter sigma, Σ, will be
used to stand for "the sum of." For example, ΣX
identifies the sum of the scores.





