Psychology 230

Z-Scores

I. z-scores and location in a distribution

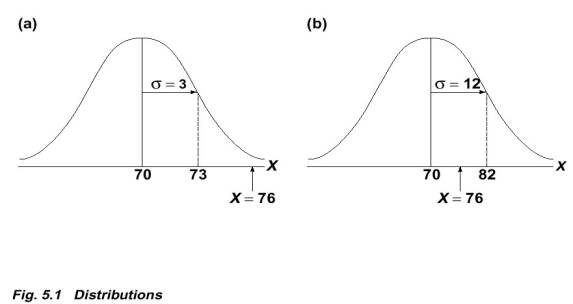
A. What is a z-score?

- standardize a distribution

 uses mean and st. dev. to produce a number

- sign (+ or -) indicates above or below mean

- number gives distance from mean in st. dev. units

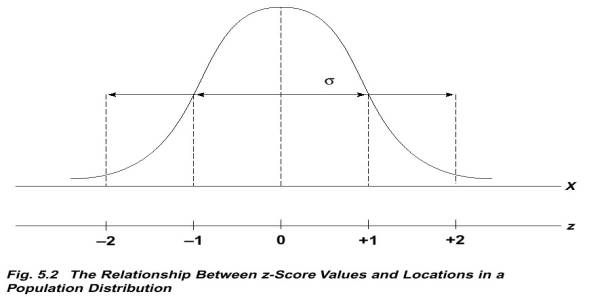
- Thus, a score that is located two standard deviations above the mean will have a z-score of +2.00.  And, a z-score of +2.00 always indicates a location above the mean by two standard deviations.

 

B. Formula

 

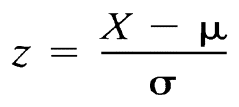
C. Deriving a raw score from a z-score

X = m + zs

 

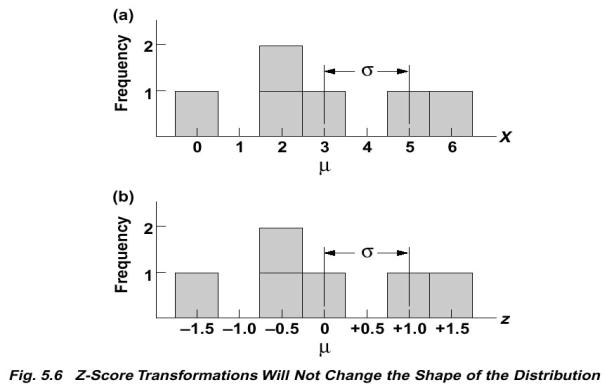
D. Characteristics of the z-score distribution

- shape will be same as the distribution of raw scores

- mean will always equal 0

- st. dev. will always equal 1

II. Using z-scores for making a comparison

A. Standardized Distribution

- transposed scores

- make dissimilar comparable

- "standard score"

B. Why are z-scores important?

- probability (ch. 6)

- evaluating treatment effects (ch. 8)

- measuring relationships

III. Other Standardized scores based on z-scores

A. Transformed Distributions

B. Steps for Transforms

- raw score to z-score (need old  m and s )

- z-score to new X score in new distribution with pre-determined mean and standard deviation (need new m and s )

 The original distribution with µ = 57 and σ = 14 was standardized to produce a new distribution with µ = 50 and σ = 10. Note that each individual is identified by an original score, a z-score, and a new, standardized score. For example, Joe has an original score of 43, a z-score of –1.00, and a standardized score of 40.