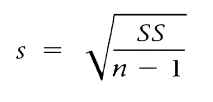
Intro. to t-Statistic
 and the Single Sample t-Test

I. Introduction

Conceptually, t = observed difference between the two means / difference expected by chance

A. The t-statistic is a substitute for z  (z is same as t except z requires more information about the population. We rarely have much information about the population, so we end up using t much more often than z.

- to use z, you must know- s (the population standard deviation)

- what do you do if you don't know s ?

- t statistic allows you to use sample standard deviation - s - instead of s
Remember that S² = SS/n - 1
SO

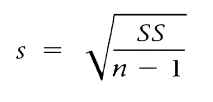
Remember:      because sometimes we'll be given SS, but other times we'll need to calculate SS ourselves

- then use estimated standard error for a sample - S xbar or S_M

      or more direct way is to use variance in calculating estimated standard error, so S_M = sqrrt of S²/n

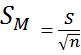
- use a t statistic instead of a z statistic (very similar formula)

t = M-µ/ S_M   where 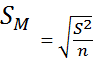    or  

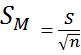
- Rule - if you know the population standard deviation, use z. If you do NOT know the population standard deviation, use t.

B. Degrees of Freedom

- df = n - 1

- the greater n is, the more closely S represents s, and then the better t represents z

C. t distribution

- generally not normal - flattened and stretched out

- approximates normal in the way that t approximates z

- shape determined by df

- Table B.2 shows critical values for the t-statistic is on p. 703

II. Hypothesis Testing with t statistic--Single Sample t-test

A. Formula

t = M-µ/ S_M    where 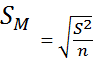    or  

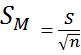
B. Steps (just like z)

n = 16 birds, µ = ?, s = ?  We need to estimate µ and s.

M = 39 minutes on the plain side and SS = 540

Do birds spend equal amounts of time in the plain chamber and the chamber with eyespots? Use a 2-tailed test and set alpha at .05.

 1) State the hypotheses.

2) Locate the critical region of the t-distribution

3) Calculate the t-statistic

4) Make a decision regarding the null and alternative hypotheses.