Psychology 231

Stats/Methods I 

Percentiles, Percentile Ranks, and Interpolation (GW 2)

I. Percentiles and Percentile Ranks

Percentile Rank - the percentage of individuals in the distribution with scores at or below the particular value.

Percentile - the particular score (X) associated with a percentile rank. 

     E.g., You scored X=4 on the test (see the distribution below). You know that roughly 85% of the class had scores of 4 or lower. 

 

Your score has a percentile rank of ____.

Your score of ____ would be called the 85th percentile.

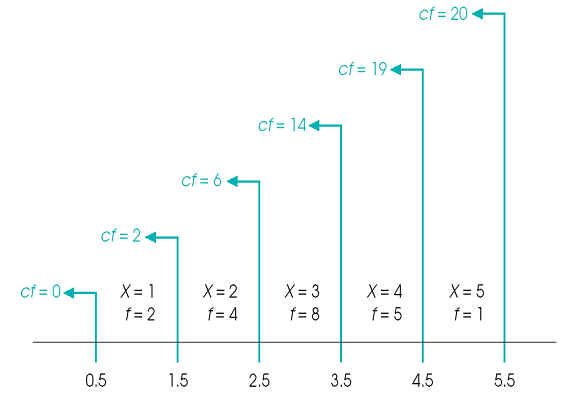
Cumulative frequencies (cf) show the number of individuals located at or below each score

To find percentiles, we must convert these frequencies into percentages.

- The percentages that result are called cumulative percentages (c%)--show the percentage of individuals accumulated as you move up the scale

              X     f      p       %         cf    c%

              5     3     .15    15%     20   100%

              4     4     .20    20%     17   85%

              3     8     .40    40%     13   65%

              2     3     .15    15%     5     25%

              1     2     .10    10%     2     10%

 

Now consider example 2.5 on p. 53

Remember that the X values in the table are not points on a scale, but intervals

Each cumulative percentage value is associated with the upper real limit of its interval

Figure 2-13  (p. 53)
The relationship between cumulative frequencies (cf values) and upper real limits. Notice that two people have scores of X = 1. These two individuals are located between the real limits of 0.5 and 1.5. Although their exact locations are not known, you can be certain that both had scores below the upper real limit of 1.5.

 

 

II. Interpolation

 

 

 

 

A Graphic Representation of Interpolation

 

 

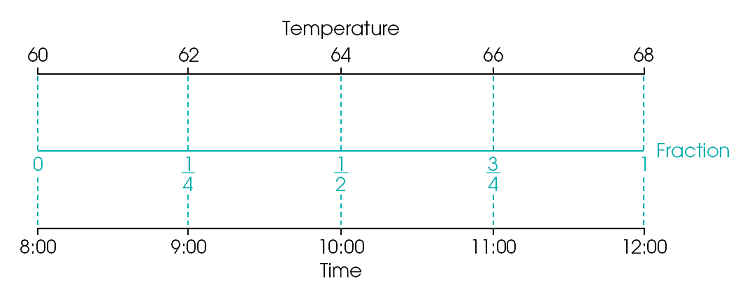
Figure 2.14  (p. 55)  The graphic representation of the process of interpolation. The same interval is shown on two separate scales, temperature and time. Only the endpoints of the scales are known – at 8:00 the temperature is 60 degrees and at 12:00 the temperature is 68 degrees. Interpolation allows you to estimate values within the interval by assuming that fractional portions of one scale correspond to the same fractional portions of the other. For example, it is assumed that halfway through the temperature scale corresponds to halfway through the time scale.
 

 

4 Steps for Interpolation

  1. Find the width of the interval on both scales

  2. Locate the position of the intermediate value in the interval. What fraction of the whole interval?
    fraction = distance from top of interval/interval width

  3. Use fraction to determine the distance from the top of the interval for the other scale
    distance = fraction x width

  4. Use distance from top to determine the position on the other scale