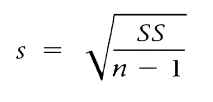
Intro. to t-Statistic
 and the Single Sample t-Test

I. Introduction

A. t-statistic is a substitute for z

- to use z, you must know- s

- what do you do if you don't know s ?

- t statistic allows you to use sample standard deviation - s - instead of s
Remember that S² = SS/n - 1
SO

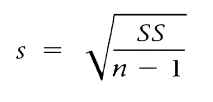
Remember:      because sometimes we'll be given SS, but other times we'll need to calculate SS ourselves

- then use estimated standard error for a sample - S xbar or S_M

      or more direct way is to use variance in calculating estimated standard error, so S_M = sqrrt of S²/n

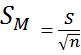
- use a t statistic instead of a z statistic (very similar formula)

t = M-µ/ S_M   where 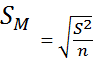    or  

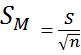
- Rule - if you know the population standard deviation, use z. If you do NOT know the population standard deviation, use t.

B. Degrees of Freedom

- df = n - 1

- the greater n is, the more closely S represents s, and then the better t represents z

C. t distribution

- generally not normal - flattened and stretched out

- approximates normal in the way that t approximates z

- shape determined by df

- Table B.2 shows critical values for the t-statistic is on p. 729

II. Hypothesis Testing with t statistic--Single Sample t-test

A. Formula

t = M-µ/ S_M    where 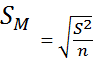    or  

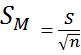
B. Steps (just like z)

Try this:

A psychologist would like to determine whether there is a relation between depression and aging. It is known that the general population averages m= 40 on a standardized depression test. The psychologist obtains a sample of n = 36 individuals who are over the age of 70. The average depression score for this sample is M = 44.5 with SS = 5040. On the basis of this sample, can the psychologist conclude that depression for elderly people is significantly different from depression in the general population? Use 2-tailed test at the .05 significance level.