Psy 633 Calculating Two-Factor ANOVA (Independent Measures)

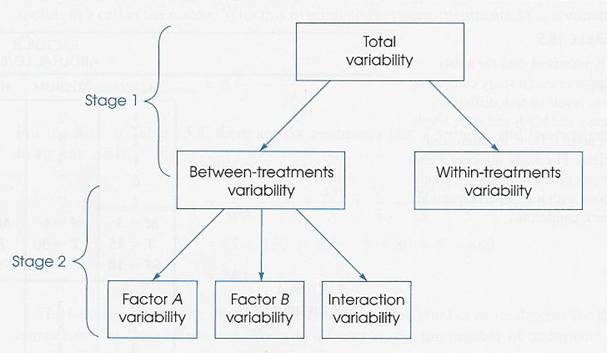
I. Partitioning Variability

A two-factor ANOVA tests for mean differences occurring in three locations:

    1.  Mean differences between levels of Factor A

    2.  Mean differences between levels of Factor B

    3.  Mean differences between unique combinations of the two factors (an A x B interaction)

II. Understanding & Describing the Factorial Effects

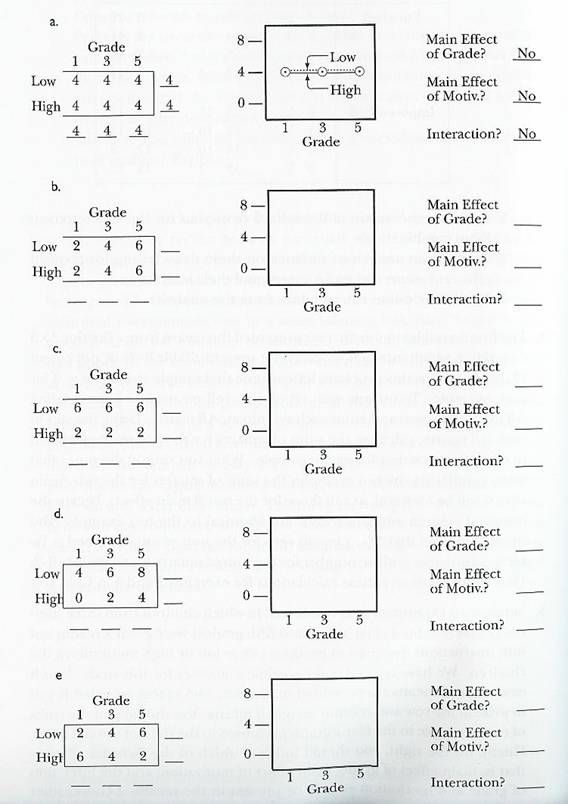
Suppose an experiment was conducted in which children from three different grades in school (first, third, and fifth grades) were given a reading test with instructions designed to produce either low or high motivation in the children. Possible outcomes of the study are presented below. In each case, the cell means are presented on the left, with spaces provided for you to write in the row and column means. You should plot the results of each example in the blank graph presented to the right of the cell means. Finally, indicate which of the factorial effects—main effect of grade, main effect of motivation, and the interaction of grade and motivation—appear to be present in the results.

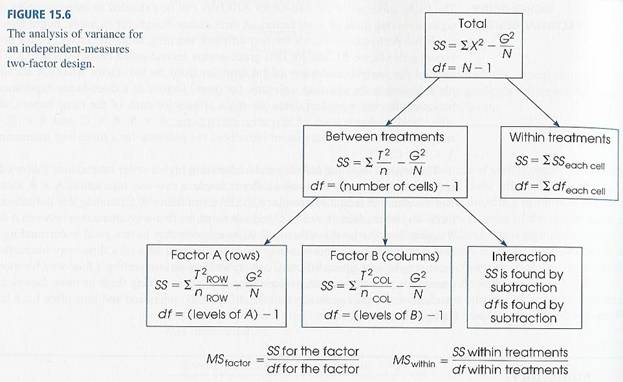
III. Conducting the ANOVA

IV. Calculating Effect Size

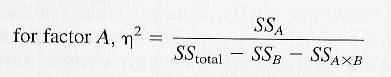
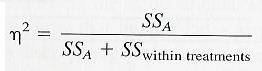
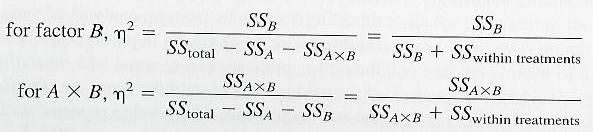
V. Example

Hyperactivity in children usually is treated by counseling, drugs, or both.  The data in the link are from an experiment designed to evaluate the effectiveness of these different treatments.  The dependent variable is a measure of attention span (how long each child was able to concentrate on a specific task).     The data and hand calculations are here.                    Table of critical values

VI. Interpreting the Interaction

Whenever a two-factor ANOVA produces a significant interaction, you should use the interaction, not the main effects, as the basis for interpreting the results.

    A.  Simple Main Effects

We can use a statistical analysis to evaluate the separate components of the interaction. These analyses ask questions about specific mean differences within the interaction. We test the significance of mean differences within one column (or one row) of a two-factor design.

For example, do non-obese participants eat significantly more when they are hungry than when they are full?

Also, when participants have full stomachs, do the obese participants eat significantly more than the non-obese participants?

The analysis is essentially a single-factor ANOVA. Compute MS_{Between Treatments} as if the two groups were the only two in the experiment. Use MS_{Within Treatments} from the original two-factor ANOVA.