Rate Theory, GC and HETP (Packed Columns)

The rate theory derives the Van Deemter Equation in terms of the properties of the chromatographic column, and takes the form;

where A, B and C are constant for a column, where experimental parameters remain unaltered during the run. Chromatographic columns with small H values bring about compact peaks.

Rate theory considers the on column broadening of the chromatographic to arise from,

a. unevenness of the mobile phase flow

b. longitudinal diffusion of analytes along the column

c. resistance to mass transfer in between the phases of the analyte

a. Eddy Diffusion: The inert support material used in packed columns, under ideal conditions are spheres of equal size. However in practical terms they are neither spheres nor uniform in size. Thus we can only use the term average particle diameter for the inert material particles, d_p. As a consequence of the particle size distribution the packing in column will be uneven. Streams of mobile phase moving through such a column would travel different path lengths (Eddy diffusion); longer path lengths will vary depending on the degree of packing. Therefore the analyte in the mobile phase in different regions will move different distances; this difference in lengths traveled by the same analyte will contribute to its band broadening. In a collection of particles of uneven size, the non-uniformity of packing is proportional to its average size. Therefore Eddy diffusion is proportional to d_p.

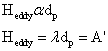
To minimize the contribution to H by eddy diffusion, H_eddy, smaller particles could be used as the support material. This will render the need for high pressure gradients to force the mobile phase through the column.

b. Longitudinal Diffusion: It is a natural tendency for material to move from high concentration zones to low concentration zones. At the injection point the analyte is concentrated to a very small region in the column. This generates a concentration gradient at the edges of the plug. The plug of analyte will diffuse on either side of the x-direction , the rate of which (flux, J) is given by the Fick's first law of diffusion.

where D = diffusion coefficient of the analyte and c = concentration. The solution of which yields for the concentration distribution over time t and space x as,

Above relationship is a Gaussian function of standard deviation, sigma. The diffusion in the mobile phase is much larger than that in the stationary phase. The time spent by the analyte in the mobile phase is L/u, where L = length of the column. Substituting in the above equation,

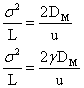
after incorporating the obstruction factor, gamma, (~1). By definition,

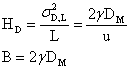
The above form makes good sense because larger diffusion constants and slow mobile phase velocities (i.e. large t_R) will tend to increase the band broadening via diffusion.

c. i. . Stationary phase mass transfer effect: The equilibration of analyte molecules between the phases is not instantaneous in real situations. Instantaneous equilibrium is desirable but not achieved. The constant motion of the mobile phase, carrying a fraction of the analyte, brings out the effect due to 'slow' equilibration rate. The movement of the mobile phase coupled with slower equilibration of molecules between the phases, makes molecules leaving the stationary phase into the mobile phase lag behind those in the mobile phase. This results in the analyte occupying a larger space, i.e. spreading of the band. The rate of equilibration can be enhanced by the length of the path of diffusion of the molecules in the stationary phase. Practically it is achieved by lowering the stationary phase thickness, d_f. Rate of equilibration is inversely related to the diffusion constant of the analyte in the stationary phase, D_S. Lower mobile phase velocities will also permit better equilibration. Further the volumes of the phases and the concentrations of analytes in the phases will play a role in determining the rate of equilibration. Such factors will be incorporated via k'. The overall effect on the HETP, H_stat is;

To minimize H_stat the factors k', and d_f can be lowered. This will effect in reduced capacity of the column to handle even moderately large sample sizes. Decreasing u will also have a detrimental effect because it affects H_D adversely.

ii. Mobile phase mass transfer effect: The mobile phase moves through as a multitude of streams. The higher the number of streams the faster is the attainment of equilibrium between the phases. Smaller size inert particles will accomplish the desired multitude of streams. The smaller sized particles will also reduce the size of pores inside the particle, making any stagnation of analyte molecules in the pores minimal. The higher diffusion coefficients, D_M, in the mobile phase and lower u facilitate the rate of attainment of equilibrium. The mobile phase mass transfer resistance effect on HETP is given by;

The net HETP due to mass transfer effect is,

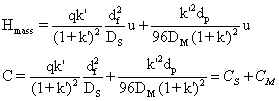
The HETP from the on column effects would then be;

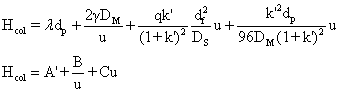
Apart from the processes on the column, extra-column effects contribute to the observed H. The analyte plug takes a finite time to move through the injector and the detector. The contributions to the final sigma value of the chromatographic peak from the finite time of residence in the injector and the detector are;

where t = time spent by the analyte zone in the respective regions. The HETP from extra-column effects, a constant for a given set column, will then be;

The effective overall H will then be,

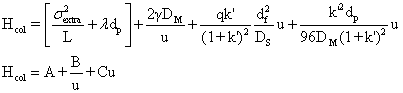
The value of u at minimum value of H is,

and the minimum value of H is

.