2.5.2 SAS Postulate
![]() Printout
Printout
—![]() Eric
Eric
Postulate 15.
(SAS Postulate) Given a one-to-one correspondence between two
triangles
(or between a triangle and itself). If two sides and the included angle of the
first triangle are congruent to the corresponding parts of the second triangle,
then the correspondence is a congruence.
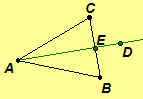
We restate the Crossbar Theorem here since it plays an important role in the
proofs of some of the results in this section.
Theorem
2.9. (Crossbar Theorem) If ![]()
![]()
![]()
![]()
![]()
Definition.
An isosceles triangle is a
triangle
with two congruent sides. If the isosceles triangle has exactly two congruent
sides, the angles opposite the two congruent sides are called base angles,
the angle formed by the two congruent sides is called the vertex angle, and the third noncongruent side is called the
base.
An equilateral triangle is a
triangle with all sides congruent.
A
scalene triangle has no congruent sides.
![]() Theorem 2.10. (Pons Asinorum) The base angles of an isosceles triangle are
congruent.
Theorem 2.10. (Pons Asinorum) The base angles of an isosceles triangle are
congruent.
Pons
Asinorum (![]() Proposition
5 from Book 1 of Euclid's
Proposition
5 from Book 1 of Euclid's
![]() Elements.
The name comes from the diagram, which looks like a bridge, used in
Elements.
The name comes from the diagram, which looks like a bridge, used in ![]()
Proof.
 Let
Let ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Exercise 2.48.
Find
the axiom from a high school book that corresponds to the SAS Postulate.
Exercise
2.49. Show the SAS Postulate is not satisfied by the (a)
Taxicab plane;
and (b) Max-distance plane. Thus showing independence.
Exercise
2.50. Prove or disprove. If quadrilateral ABCD is such that
BD
and AC intersect at a point M and M is the midpoint of both
BD and
AC, then
AB is
congruent to
CD.
Exercise
2.51. Prove or disprove. If quadrilateral ABCD has
CD congruent
to CB and ray CA is the bisector of ![]()
![]()
![]()
![]()
![]()
Exercise
2.52. Prove or disprove. If ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Exercise
2.53. State and prove each theorem.
(a) SSS Theorem; and (b) ASA
Theorem.
Exercise
2.54. Prove that all points equidistant from two points A and B are on the perpendicular
bisector of
AB.