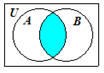
The Venn diagram for
A
∩ B is shown to the right
where the shaded region
represents the set
A
∩ B.
The Camtasia Studio video content presented here requires JavaScript to be enabled and the latest version of the Macromedia Flash Player. If you are you using a browser with JavaScript disabled please enable it now. Otherwise, please update your version of the free Flash Player by downloading here.
Intersection:
The set operation
intersection takes only the elements that are in both sets.
The intersection contains the elements that the two sets
have in common. The
intersection is where the two sets overlap.
In set-builder notation, A
∩ B = {x
∈
U :
x
∈
A and
x
∈
B}.
|
The Venn diagram for
A
∩ B is shown to the right
where the shaded region
represents the set
A
∩ B. |
|
Example:
Let
A = {a,
b, c, d} and B = {b,
d, e}. Then
A
∩ B
= {b,
d}.
The elements b and
d are the only
elements that are in both sets
A and
B.
Example:
Let
G = {t,
a, n} and H = {n, a, t}. Then
G
∩ H = {a,
n, t}. Note that here
G =
H =
G
∩ H.
Example:
Let
C = {2, 6, 10, 14, …}
and D = {2, 4, 6, 8,
…}. Then
C
∩ D = {2, 6, 10, 14, …}
= C.
Example:
Why is the location where a
street and an avenue cross called an
intersection? The location is contained in both the street and the
avenue.
Example:
Let
E = {d, a, y} and F = {n,
i, g, h, t}.
Then E
∩ F =
∅.
Note:
In all the examples, the
intersection is a subset of each set forming the intersection,
i.e., A
∩ B
⊆
A and
A
∩ B
⊆
B.
Disjoint Sets:
Two sets whose
intersection is the empty set are called
disjoint sets.
Example: Let E = {d, a, y} and F = {n, i, g, h, t}. Since E ∩ F = ∅, the sets E and F are disjoint sets.