The Camtasia Studio video content presented here requires JavaScript to be enabled and the latest version of the Macromedia Flash Player. If you are you using a browser with JavaScript disabled please enable it now. Otherwise, please update your version of the free Flash Player by downloading here.
The following set properties are
given here in preparation for the properties for addition and
multiplication in arithmetic. Note the close similarity between
these properties and their corresponding properties for addition
and multiplication.
Commutative
Properties:
The
Commutative Property for Union
and the
Commutative Property for Intersection
say that the order of the sets in which we
do the operation does not change the result.
General Properties:
A
∪
B =
B
∪
A
and
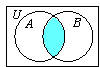
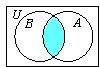
A
∩
B =
B
∩ A.
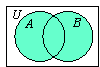

Example:
Let
A = {x
: x is a whole number
between 4 and 8} and B
= {x :
x is an even natural
number less than 10}.
Then A
∪
B = {5, 6, 7}
∪
{2, 4, 6, 8} = {2, 4, 5, 6, 7, 8} = {2, 4, 6, 8}
∪
{5, 6, 7} = B
∪
A
and
A
∩ B = {5, 6, 7}
∩ {2, 4, 6, 8} = {6} = {2, 4, 6, 8}
∩ {5, 6, 7} = B
∩ A.
Associative Properties:
The Associative Property
for Union and the
Associative Property for Intersection says that how the sets
are grouped does not change the result.
General Property: (A
∪
B)
∪
C =
A
∪
(B
∪
C) and (A
∩ B)
∩ C =
A
∩ (B
∩ C)
Example:
Let A = {a, n,
t}, B = {t, a, p},
and C = {s, a, p}.
Then
and
(A
∩ B)
∩ C = {a, t}
∩ {s, a,
p} = {a} = {a, n, t}
∩ {a, p}
= A
∩ (B
∩ C)