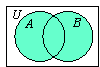Operations like addition, subtraction, multiplication, and division are numeric operations. These numeric operations work with numbers and produce numeric solutions. 

Example:  The equation 4 + 3 = 7 illustrates a numeric operation where the operation is addition.

        In contrast, operations with sets (set operations) work with sets and have sets for answers.  The set operations we will work with in this session are union and intersection.

 Union:  The set operation union brings together all of the elements of both sets whether those elements are in one or both of the sets.      

In set-builder notation,   A ∪ B = {x ∈ U : x ∈ A or x ∈ B}. 

The Venn diagram for A ∪ B is shown to the right where the shaded region represents the set  A ∪ B.

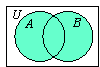Example:  Let A = {a, b, c, d} and B = {b, d, e}.  Then A ∪ B = {a, b, c, d, e}. The Venn diagram illustrates the result.
                                              
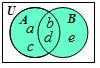
The elements b and d are not written twice in the union even though they are in both sets.  Remember that in the roster notation for sets we do not repeat elements within the set braces. 

Example:  On campus, why is union used in the name of the Comstock Memorial Union (CMU)?  The CMU is a place where all members of the campus may gather or come together, a union of all groups (sets) of students, faculty, and staff on campus. 

Example:  Let G = {t, a, n} and H = {n, a, t}. Then G ∪ H = {a, n, t}.
                   Note that here G = H = G ∪ H. 

Example:  Let C = {2, 6, 10, 14, …} and D = {2, 4, 6, 8, …}.
                   Then C ∪ D = {2, 4, 6, 8, …} = D.   

Example:  Let E = {d, a, y} and F = {n, i, g, h, t}.
                   Then E ∪ F = {d, a, y, n, i, g, h, t}.

Note:  In all the examples, each set forming the union is a subset of the union, i.e. A ⊆ A ∪ B and B ⊆ A ∪ B.