The Camtasia Studio video content presented here requires JavaScript to be enabled and the latest version of the Macromedia Flash Player. If you are you using a browser with JavaScript disabled please enable it now. Otherwise, please update your version of the free Flash Player by downloading here.

        Many of the procedures we use to perform arithmetic with whole numbers follow directly from the nature of our place value system (Hindu-Arabic numeration system). 

       For instance, when we use the Standard Algorithm for Addition, why do we line up the addition of whole numbers so that the numerals are “right justified”?  The reason, we line up the columns for the addition of whole numbers, follows from the concepts of the union of disjoint sets and place value.

Example:     456,090 + 4,593 + 12,079 + 300

We illustrate the problem by using sets and denominations of money.

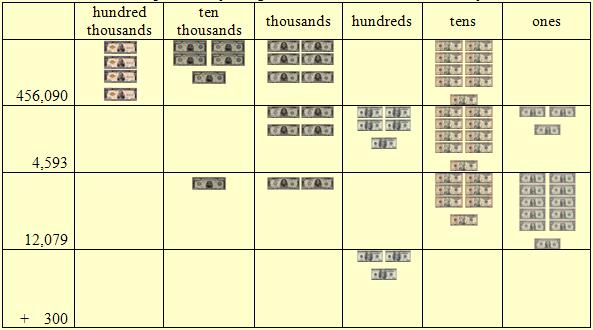
Currency illustration of the example.

            We use the above example to illustrate how the place value system and the union of sets demonstrates the step-by-step procedure of the Standard Addition Algorithm. 

     456,090  
         4,593     
       12,079
  +        300

           We begin adding the column farthest to the right and then when the total exceeds 9, we exchange each set of ten 1’s for a ten and place it in the next column. The concept is the same as when we combine the sets of $1-bills and, when possible, convert them to $10-bills. The whole procedure is this grouping 10’s and placing them in the correct place value.  Different people give different names for this procedure; some call it “regrouping”, “exchanging”, “trading”, or “carrying”.

               1
     456,090  
         4,593     
       12,079
  +        300
                 2

           We add the ones column to obtain 12, e.g., 0 + 3 + 9 + 0 = 12. That is, we have combined the dollar bills to obtain twelve dollars and then exchanged ten $1-bills for one $10-bill. The 2 for the remaining two dollars is written at the bottom of the column and the 1 for the $10-bill is written at the top of the tens column.
$1 bill$1 bill$1 bill
$1 bill$1 bill$1 bill$1 bill$1 bill$1 bill$1 bill$1 bill$1 bill
Exchange ten $1-bills for one $10-bill.
$10-bill$1 bill$1 bill

             21
      456,090  
         4,593     
       12,079
  +        300
               62

           We next add the ten’s column, 1 + 9 + 9 + 7 + 0 = 26. We have combined the $10-bills to obtain 26 $10-bills and then exchanged twenty of them for two $100-bills. The 6 for the remaining $10-bills is written at the bottom of the column and the 2 for the $100-bills is written at the top of the hundreds column.
$10-bill
$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill
$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill
$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill
Exchange twenty $10-bills for two $100-bills.
$100-bill.$100-bill.$10-bill$10-bill$10-bill$10-bill$10-bill$10-bill

          1 2 1
     456,090  
         4,593     
       12,079
  +        300
            062

           We next add the hundred’s column, 2 + 0 + 5 + 0 + 3 = 10. We have combined the $100-bills to obtain 10 $100-bills and then exchanged them for one $1000-bill. Since there are no $100-bills remaining, we record a 0 at the bottom of the column. We record a 1 at the top of the thousands column for the one $1000-bill.
$100-bill.$100-bill.
$100-bill.$100-bill.$100-bill.$100-bill.$100-bill.
$100-bill.$100-bill.$100-bill.
Exchange ten $100-bills for one $1000-bill.
$1,000-bill.

        11  21
     456,090  
         4,593     
       12,079
  +        300
         3,062

           We next add the thousand’s column, 1 + 6 + 4 + 2 = 13. We have combined the $1000-bills to obtain 13 $1000-bills. We exchange ten of them for one $10,000-bill. The 3 for the remaining $1000-bills is written at the bottom of the column and the 1 for the $10,000-bill is written at the top of the ten-thousands column.
$1,000-bill.
$1,000-bill.$1,000-bill.$1,000-bill.$1,000-bill.$1,000-bill.$1,000-bill.
$1,000-bill.$1,000-bill.$1,000-bill.$1,000-bill.
$1,000-bill.$1,000-bill.
Exchange ten $1,000-bills for one $10,000-bill.
$10,000-bill.$1,000-bill.$1,000-bill.$1,000-bill.

        11  21
      456,090  
         4,593     
       12,079
  +        300
       73,062

           We next add the ten-thousand’s column, 1 + 5 + 1 = 7. We have combined the $10,000-bills to obtain 7 $10,000-bills. Since we have less than ten of them, we are unable to make any exchanges. So, we record the 7 at the bottom of the column.
$10,000-bill.
$10,000-bill.$10,000-bill.$10,000-bill.$10,000-bill.$10,000-bill.
$10,000-bill.
No exchanges are possible.

        11  21
     456,090  
         4,593     
       12,079
  +        300
     473,062

           Finally, since there is only a 4 in the hundred-thousand’s column, we write it at the bottom of the column. Since there were only 4 $100,000-bills, we had none to combine. So, we keep those bills.
$100,000 bill.$100,000 bill.$100,000 bill.$100,000 bill.
No exchanges are possible.

Hence, 456,090 + 4,593 + 12,079 + 300 = 473,062.