Readings for Session 7 – (Continued)  

Union of Sets and Addition

How does the operation of addition used in the following problem relate to sets?

 Sam had two savings accounts. He had $836 in one account and $429 in another account. How much money did Sam have in savings?

        The first account is a set of dollars where the whole number 836 represents the cardinality of the set and the second account is a set of dollars with a cardinality of 429. The two accounts are distinct; hence, the two sets do not have any elements (dollars) in common. The addition, $836 + $429 = $1,265, gives a new whole number that represents the cardinality of a new set which is the union of the two disjoint sets (accounts).
        In this section, we illustrate the relationships between the addition of whole numbers and the union of sets. We show a difference in the process of addition when the two sets are disjoint and when their intersection is not the empty set.

        Andy has two airplanes and Billy has three airplanes. How many airplanes do they have all together?

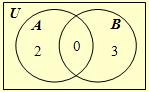
In the picture and the Venn diagram, there are two sets A and B. Notice that the sets are disjoint, n(A) = 2, n(B) = 3, and n(A ∪ B) = 2 + 3 = 5.

        Ann has $12 available to spend and Bob has $16 available to spend.  But, $7 of their money is in a joint account.  How much money do they have all together?

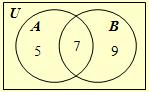
In this Venn diagram, there are two sets A and B. Notice that the sets are not disjoint, n(A) = 12, n(B) = 16,
but now (A ∪ B) = 21 ≠ 12 + 16 = 28.

Can you explain why you cannot just add 12 and 16 to find the total?

        Notice that  n(A ∪ B) = n(A) + n(B) − n(A ∩ B) and this formula works for both of the Venn diagram situations above.  We will see this relationship again when we study probability.

        The above problems involving sets motivate the following definition for addition of whole numbers.

Addition of Whole Numbers:  Let a = n(A) and b = n(B) where A and B are two disjoint finite sets. Then a + b = n(A ∪ B).

The whole numbers a and b are called addends and the result a + b is called the sum. (Reminder: n(A) represents the cardinal number for set A.)

Important Note. The sets A and B must be disjoint sets, i.e., A ∩ B = ∅.

   

      

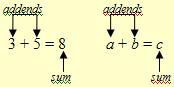Return to Peil's Homepage | Minnesota State University Moorhead | Mathematics Department