Readings for Session 9 – (Continued)  

Fundamental Counting Principle

Fundamental Counting Principle

 

        The Cartesian product form for multiplication is the basis for the Fundamental Counting Principle.  This principle tells us that if there are “a” ways to do task A and “b” ways to do another task B, there are a × b ways to do task A followed by task B.

Example: You have three t-shirts and two pairs of shorts.  In how many ways can you choose one t-shirt and one pair of shorts to wear?

Answer: We have two distinct sets of objects, t-shirts (T) and shorts (S). 

3 × 2 = n(T) ∙ n(S) = n(T × S) = 6

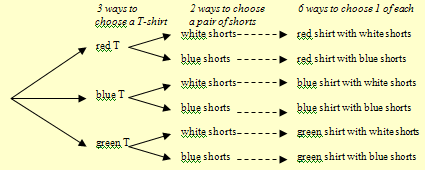
You have six choices for an outfit of one t-shirt and one pair of shorts.

       Notice that the tree diagram for the above problem was easily drawn out as a tree diagram to illustrate all the ordered pairs of t-shirts and shorts. But, for problems with a large number of objects, the Fundamental Counting Principle gives a short-cut way of counting the number of end-branches in a tree diagram without needing to draw out the entire diagram.  

Example:   A coin is tossed, a die is rolled, and a card is drawn from a standard deck. How many outcomes are possible?

Notice that a tree diagram for this problem would take a lot of time to draw out with all the possibilities. So, we apply the Fundamental Counting Principle to count all the ordered triplets for the coin, die, and card such as
(H, 3, ace of hearts) or (T, 2, queen of clubs).

n(coin) ∙ n(die) ∙ n(card) = 2 ∙ 6 ∙ 52 = 624

There would 624 possible outcomes when a coin is tossed, a die is rolled, and a card is drawn.

    

      

Return to Peil's Homepage | Minnesota State University Moorhead | Mathematics Department