Readings for Session 12 – (Continued)
Factors, Multiples, and Divisors
Factors,
Multiples, and Divisors:
Two numbers are factors
of a number if there product is the number. The number is a
multiple of a factor.
Each factor is a divisor
of the number.
General Property when the Natural Numbers is the Universal Set:
a is a
factor of b if there is a
k so that
b = ak with {a, b, k}
⊆
N.
b is a
multiple of a if there is
a number k so that
b = ak with {a, b, k}
⊆
N.
a is a
divisor of
b if there is a k so that
b = ak with {a, b, k}
⊆
N.
Numeric Example:
Since 5
× 8 = 40, both 5 and 8 are factors
of 40.
Since 5
× 8 = 40, 40 is a
multiple of 5 and 40 is also a
multiple of 8.
Since 5
× 8 = 40, both 5
is a divisor of 40 and 8 is also a
divisor of 40.
Often we need to find all of the factors or
multiples of a number. It is convenient to think of this group
of factors as a set.
Example:
In the introduction problem, the question was asking for
all the natural number factors of twelve. The set of factors of
twelve, {1, 2, 3, 4, 6, 12}, is a list of possibilities for the
number of people who would receive gumballs.
Examples:
The set of all the whole number factors of 15 is {1, 3, 5, 15}.
The set of all the whole number divisors of 15 is {1, 3, 5, 15}.
The set of all the natural number multiples of 15 is {15, 30, 45, 60, …, 15n, …}.
The set of all the whole number
multiples of 15 is {0, 15, 30, 45, 60, …, 15n,
…}.
Note that the universe affects the
answer. Zero is a whole number multiple of every number since 0
×
a = 0. Also notice
that the set of multiples is an infinite set.
Examples:
{x :
x is a natural number
multiple of 4} = {4, 8, 12, 16, 20, 24, …, 4n,
…}
{x :
x is a whole number multiple of 4} = {0, 4, 8, 12, 16, 20, 24, …, 4n,
…}
Examples: {x : x is a natural number factor of 24} = {1, 2, 3, 4, 6, 8, 12, 24}.
{x : x is a whole number factor of 24} = {1, 2, 3, 4, 6, 8, 12, 24}.
{x : x is a natural number divisor of 24} = {1, 2, 3, 4, 6, 8, 12, 24}.
{x :
x is a whole number divisor of 24} = {1, 2, 3, 4, 6, 8, 12, 24}.
Note that the set of factors is the same when the
universe is either the natural numbers or the whole numbers.
If we are asked
for the set of all factors of a value, we MUST include all the
whole number factors for the set to be the correct answer.
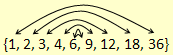
Notice that the factors generally come in pairs.
![]()
Return
to Peil's Homepage | Minnesota
State University Moorhead | Mathematics
Department