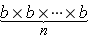Exponents and Simplifying Expressions

Motivation for Exponents

Which would you choose?

You are given an option of being paid either

• $1,000,000 or

• for thirty days receiving one cent the first day and each succeeding day double the amount of the previous day.

How much would you receive on the 30^th day?

The double of an amount is the same as multiplying an amount by two. So, the daily amounts in cents for each day would be:

Day 1               1¢
Day 2               2¢
Day 3               2 × 2 = 4¢
Day 4               2 × 2 × 2 = 8¢
Day 5               2 × 2 × 2 × 2 = 16¢
Day 6               2 × 2 × 2 × 2 × 2 = 32¢
Day 7               2 × 2 × 2 × 2 × 2 × 2 = 64¢

This is getting to be a lot of multiplications to write. We use exponents to write the problem for each day in a shorter form. Since Day 7 has two used as a factor six times, we may write the problem as

Day 7               2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64¢

Then Day 8 would use another factor of 2 for

Day 8               2⁷ = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128¢
Day 9               2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256¢
Day 10           2⁹ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 512¢

We note that the number of two's used as a factor is one less than the number of the day, so

Day 30           2²⁹.

This says that we would need to multiply 29 two's to find the amount of money in cents for the thirtieth day. Determine this amount then decide which choice would be the best choice.

Solution

The above problem motivates why exponents are used as a shortcut to setup problems. We now give more examples involving exponents.

Exponents

Definition of an Exponent: The expression 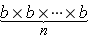, which is n factors of b used for n – 1 multiplications, can be written as bⁿ.  The b is called the base and the n is called the exponent.

Examples:

1. A coin is flipped three times. How many outcomes are possible?
   To solve the above problem in Session 9 (Old Session 9), we completed a tree diagram (as illustrated below) to solve the problem to motivate the Fundamental Counting Principle.
   
   Note that we could also express the problem in exponential form as
   2³ = 2 × 2 × 2 = 8.
   We have eight possible outcomes when a coin is flipped three times.
   
2. What if we were to flip a coin four times? How many outcomes are possible?
   Setting up the problem using exponents, we obtain 2⁴ = 2 × 2 × 2 × 2 = 16. There would be sixteen possible outcomes if a coin is flipped four times.
   
3. If we flip the coin thirteen times, then 2¹³ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 8,192. We would have 8,192 different possible outcomes if a coin is flipped thirteen times.

Note that as the number of times we have to repeat the multiplication becomes larger, the notation of using only multiplication becomes cumbersome. So, we use the short-cut notation with exponents to represent this type of repeated multiplication.

Example:   In 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2, the 2 is repeated 13 times.

More Examples:

1. 3² = 3 × 3 = 9
   
2. Use repeated multiplication to find 5³, 10⁵, and 9³.
         5³ = 5 × 5 × 5 = 25 × 5 = 125
       10⁵ = 10 × 10 × 10 × 10 × 10 = 100,000
         9³ = 9 × 9 × 9 = 9 × 81 = 729
   
3. Dino is eating at his favorite Italian restaurant. On the menu there are three wines, three salads, three entrees, and three desserts. There are also three credit cards in his wallet. How many ways can he choose a meal choosing exactly one of each type of item and pay fo it with a credit card?
   We apply the Fundamental Counting Principle and use exponents to obtain
   3⁵ = 3 × 3 × 3 × 3 × 3 = 243.
   Dino has 243 choices for a meal and paying for it.

Self-Check Problem

A standard die is rolled five times. How many outcomes are possible? Write the problem in exponential form and then solve it.

Solution

Exponents and Cartesian Product

Since exponents represent repeated multiplication, exponents may also be used to represent Cartesian products of sets (the set of ordered pairs). See Session 9 (Old Session 9). For example, we may write A × A as A².

Examples:

1. A coin is flipped twice. What are the possible outcomes?
   We may solve this problem as a Cartesian product question by giving the set all the possible ordered pairs. Let C = {H, T}. Then
   C² = C × C = {(H, H), (H, T), (T, H), (T,T)}.
2. If set A = {1, 2}, then A² = A × A = {(1, 1), (1, 2), (2, 1)}.
   
3.  Let B = {0, 1, 2}. Determine the number of elements in B², check the solution by finding B², and then plot B² on a coordinate plane.

The number of elements is (n(B))² = 3² = 9. Reminder: n(B) is the cardinal number for B.  We have

B² = B × B = {(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)}.

4. Let D be the set of possible outcomes when rolling one 6-sided die. Write D using roster notation. Write out D² using roster notation. What does D² represent? How many elements are in D²?

Solutions: D = {1, 2, 3, 4, 5, 6}

D² = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

D² represents the possible outcomes of rolling a die twice or of rolling two dice.
There are 6² = 36 elements in D².

Self-Check Problem

Write the Cartesian Product for the possible outcomes of a person twice choosing one number between 1 and 3, inclusive.

Solution

Scientific Notation

Motivation Problem

The mass of a mass of the earth is approximately 6,000,000,000,000,000,000,000,000 kilograms. Scientists would write this value in scientific notation using powers of ten or exponential form. A scientist would write the mass of the earth as 6 × 10²⁴ kilograms.

Scientific notation is useful for writing very large or very small numbers. For now, we will focus on using scientific notation to write very large numbers. Consider the value three million. We typically write this number as 3,000,000, but we may also write it in scientific notation:

3,000,000 = 3 × 1,000,000 = 3 × 10⁶.

Notice that the exponent is the same as the number of zeros following the 3. Three million is a verbal expression, 3,000,000 is a decimal expression, and 3 × 10⁶ is scientific notation.

When we reviewed place value, each column of the place value chart had a place value 10 times as much as the column to the right of it. We may use scientific notation to simplify writing the values in the place value chart.

We now know three ways to express this type of number: as a standard numeral, in verbal form, and in scientific notation. Each form has its own advantages.

Examples:

Since we are only working with whole numbers, we are not writing the scientific notation with a decimal point. Later after we have worked with decimals, we will revisit scientific notation and use the normalized form for scientific notation.

Self-Check Problem

The mass of the sun is approximately 2,000,000,000,000,000,000,000,000,000,000 kilograms. Write the mass of the sun in scientific notation and the verbal form.

Solution

Multiplying Variable Expressions

Previously we learned to add variable expressions by adding like terms. Now that we have exponents, we can also multiply variable expressions. First we note that x · x = x² since the variable x has been used as a factor twice. This is just applying the definition of an exponent. Similarly, we have that a · a · a · a · a · a = a ⁶.

Now consider 3x(2x). Since everything in this expression is multiplied, we use the commutative and associative properties of multiplication with the definition of exponent to find the product:

Example: Multiply (4x)(2x)(x).

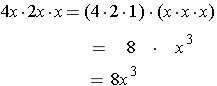
Example: Multiply (3x)(y)(x²)(5y).

Notice that coefficients are grouped together and then each different variable is grouped together.

 We note that we only add like terms and obtain like terms. But when we multiply expression with variables we do not obtain like terms , instead we get expressions with exponents. It is important to learn to make this distinction when simplifying variable expressions.

Compare each of the following when adding or multiplying the same terms.

Self-Check Problems

Evaluate each expression:

4m + 5n + m + 7n + 2m and 4m · 5n · m · 7n · 2m

Solutions

Order of Operations

Motivation Problem

Find the value of   5 + 6(4).

Unless we have specific rules for finding the above value, different people could obtain different answers. Some may multiply first then add to obtain 29 and another person might add first then multiple to obtain 44. This situation is unacceptable . So, people have agreed on certain standard rules for determining the value of expressions that involve different operations. The most common rules and the ones that we are going to use are called the algebraic order of operations. Order of operations - Wikipedia, the free encyclopedia

We have learned the operations involving exponents, division, multiplication, subtraction and addition. In order to perform complex computations with these operations properly, we need to perform these operations in a particular order. The standard rules for the algebraic order of operations are:

First, we perform operations that are grouped such as by Parentheses.
Second, we compute Exponents.
Third, we perform the Multiplication and Division from left to right.
Finally, we perform the Addition and Subtraction from left to right.

The acronym for remembering the order of operations is PEMDAS, which stands for Parentheses, Exponents, Multiplication, Division, Addition and Subtraction. A mnemonic device for remembering this acronym is Please E xcuse My Dear Aunt Sally.  

Example: The opening problem 5 + 6(4) would be worked as follows.

5 + 6(4) = 5 + 24  since multiplication comes before addition

            = 29

 A common mistake associated with this acronym is to forget that PEMDAS does not properly reflect the left-to-right part of the rules in the first paragraph. Multiplication and division have the same priority, and are done left-to-right. Addition and subtraction have the same priority, and are done left-to-right. A more accurate mnemonic might be   PE MD   AS to remind yourself that the underlined pairs are done together, moving left-to-right.

That is, multiplication and division are done in the same step, and they are done left-to-right.  

Example: In 100 ÷ 4 × 5, the multiplication and division must be done left-to-right, which means that in this case the division is actually done before the multiplication.

100 ÷ 4 × 5 = 25 × 5 = 125

In the same way, addition and subtraction are done in the same step, and they are also done left-to-right.  

Example: In 20 – 2 + 8, the addition and subtraction must be done left-to-right, which means in this case the subtraction is actually done before the addition:  

20 – 2 + 8 = 18 + 8 = 26

Examples: In each of the following the step to be done next is underlined.

Self-Check Problems

Evaluate each expression

92 – 7 · 9 Solution

7² + 4(3³ + 2) – 19 Solution

More Examples Multiplying Expressions

Consider (2x)⁴. In this case we are taking the entire product inside the parentheses to the 4^th power.

Here is another example: (ab ²)³.

Another example: (x⁴y³)².

Note that these problems are motivating the Properties of Exponents, which are methods for working these problems in a more efficient manner. Some of the Properties of Exponents will be developed later in Session 29.

Self-Check Problem

Evaluate (m²n³)⁴.

Solution

Joke or Quote

Teacher: "What is 7 times 6?"
Student: "It's 42!"
Teacher: "Very good! - And what is 6 times 7?"
Same student: "It's 24!"