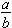, where a, b are whole numbers and b
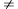0. The top numeral,a, is called the numerator and the bottom numeral, b, is called the denominator. Fraction Basics
How would you answer this question?
MSUM is hosting a six kilometer women's cross-country meet at Johnson Park on a course that is two kilometers long. Pat completed two laps. How much of the race has she completed?
There are two ways that people may state the solution to the problem. Since prior to this session we have used only whole numbers, we would probably have answered the question by saying that Pat has completed four kilometers of the race and has two kilometers left to run. But, we could also state the solution using fractions by saying that Pat has completed two-thirds of the race and has one-third of the race remaining.
Though this problem allows us to use either whole numbers or fractions to state the solution, many problems are best stated using only fractions.
So far, we have only dealt with whole numbers that are used to count how many items are in a group of items. (That is, we have been using the cardinal number of a set.) These numbers were called whole numbers because they count whole things.
In order to extend our idea of number to include parts of wholes, we use fractions such as halves, thirds, and fifths.
Fraction (mathematics) - Wikipedia, the free encyclopedia
Common Fractions: Common fractions are written in the form 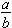, where a, b are whole numbers and b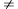0. The top numeral,a, is called the numerator and the bottom numeral, b, is called the denominator.
Note. The most proper way to write a fraction is in the vertical format, 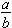. The slanted format, a/b, is for writing fractions in a typed sentence. Many students who learn to write fractions only in the slanted form have problems interpreting mixed numbers and working with rational expressions in algebra. For these reasons, your instructor may require that all fractions in this course be written in the vertical form.
Further Note. In general, the numerators and denominators of fractions may be values other than whole numbers. For example, later in this course we will need to write some fractions using integers and some fractions with decimals that are not simplified. Also, a decimal is an abbreviation of a common fraction that has a denominator that is an exponential power of ten. For simplicity, we use the term fraction even when we are talking about common fractions.
Common Fractions: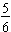 
and 
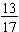
Decimal Fractions: 0.7 and 0.379 since they are the common fractions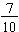 
and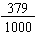 
Algebraic Fractions: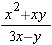 
and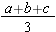 
Some Other Fractions: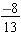 
and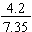 
A basic way to interpret a fraction (common fraction) is by dividing a whole object into several equal parts. The denominator tells how many equal parts the whole is subdivided into. The numerator tells the number of those parts that are under consideration.
Example:
If 
is one whole, then the shaded portion of 
is 
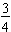of the whole. In this example, the 3 is the numerator describing the shaded part and the 4 is the denominator telling how many equal parts the whole has been divided into.
Examples: Here are several different models for the fraction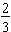 
.
Discrete model
Two-thirds of the set are shaded circles.
Number line model
The vector is two-thirds of a unit.
Area model
Two-thirds of the rectangle is shaded.
Volume model
Two-thirds of the cylinder is shaded.
Each of the fractions (in the examples on the previous page) is called a proper fraction since the fraction represents a part of a single whole object. A proper fraction is a fraction in which the numerator is less than the denominator. For example,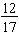 
is a proper fraction because 12 < 17.
Sometimes we need to write fractions that have more than one whole object.
For example,
each rectangle is a whole divided into four equal parts and the total shaded portions may be written as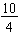 
. Since the number of equal parts is more than one whole, we call the fraction an improper fraction. An improper fraction is a fraction in which the numerator is greater than or equal to the denominator. For example, 
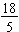is an improper fraction because 18 > 5.
Extending the above idea of improper fractions to just whole numbers, we may write every whole number as an improper fraction with a denominator of 1. For example, if each rectangle is a whole consisting of 1 part,
the 3 whole rectangles may be written as the improper fraction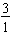 
. All whole numbers can be written in fractional notation.
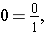
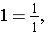
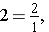
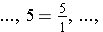
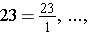
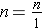
We may write the fractional notation for 1 many different ways as improper fractions.
Examples:
has a shaded portion of 1 part and may be written in fraction form as 
.
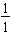has 4 equal shaded parts and may be written in fraction form as 
.
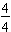There are infinitely many fractional notations for 1. If we divide an object into n parts and take n of the parts, we obtain all of the object or the whole.
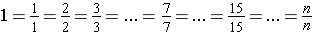
Similarly, there are infinitely many fractional notations for 0.
Examples:
has no shaded portions and may be written in fraction form as 
.
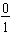has no shaded parts and may be written in fraction form as 
.
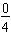If we divide an object into n parts and take none of them, we get 0.
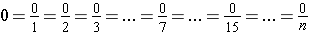
Note that by definition the denominator of a fraction is never zero, that is,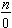 
is not defined for any whole number n. The reason is that the denominator for common fractions represents the number of equal parts a whole object is divided into and this must be at least one. A whole object cannot be divided into zero parts.
As noted before, there are an infinite number of ways to express the idea of one whole as a fraction. It turns out that there are an infinite number of ways to express any fractional part. Fractions that name the same part of the whole are called equivalent fractions.
Example:
Notice that the rectangular strips (wholes) are the same size. Also notice that the shaded portion is the same size within each strip, and the same fractional part of each strip is shaded. The difference is only in how each shaded region is named. We use an equal sign to denote equivalent fractions. By the above illustration, we have
.
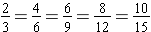Note. The numerators are multiples of 2 and the denominators are multiples of 3.
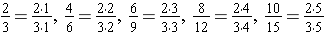
We have modeled the following property:
The Fundamental Law of Fractions Let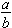 
be a fraction. Then 
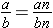, for any nonzero integer n, that is, 
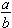is equivalent to any fraction of the form 
|
Example: |
|
Notice that the rectangles (wholes) are the same size. Also notice that the shaded portion is the same size in each, and the same fractional part is shaded in each. The difference is only in how each shaded region is named. |
The Fundamental Law of Fractions states that multiplying both the numerator and denominator of a fraction by the same non-zero whole number produces an equivalent name for the same fractional amount. For this problem, we have
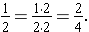
Another way of viewing this result is to remember that 
is a name for one, so in essence this is multiplying the fraction one-half by one, which gives us an equal amount. The Identity Property for Multiplication tells us that multiplication by one does not change the value of the other factor.
For the same reason, dividing both numerator and denominator by a common factor will also produce an equivalent name for the same fraction because we are essentially dividing by one. This is called simplifying a fraction. When one is the only common factor for the numerator and denominator, the fraction is in "simplest form", sometimes called "simplest terms."
Example:
As in the above examples, simplest form can be achieved by either eliminating all common factors greater than one or by dividing several times until the numerator and denominator have no common factor other than one.
A more efficient way to find the simplest form of a fraction is to use the GCF (greatest common factor) of the numerator and denominator. In the following examples, we illustrate several methods: prime factorization, factor the GCF, and divide both numerator and denominator by the GCF.
To use the prime factorization method for finding the simplest form of a fraction, we rewrite the fraction in the form with the prime factorization of the numerator and denominator. Next, rewrite the factorization with the greatest common factor as a separate factor. Finally, apply the Fundamental Theorem of Fractions to write the simplest form.
Example: Find the simplest form for the fraction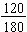 
.
We find the prime factorization for the numerator and denominator and then rewrite with the GCF written as a separate factor for the numerator and denominator. Finally, apply the Fundamental Law of Fractions.
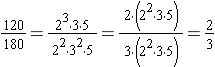
Example: Write the fraction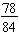 
in simplest terms.
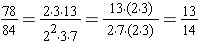
For this method, we first find the greatest common factor for the numerator and denominator. Next, rewrite the numerator and denominator each as two factors where one of the factors is the greatest common factor. Finally, apply the Fundamental Theorem of Fractions to write the simplest form.
Example: Find the simplest form for the fraction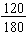 
.
We find the greatest common factor for the numerator and the denominator:
120 = 23 · 3 · 5 and 180 = 22 · 32 · 5 so the GCF(120, 180) = 22 · 3 · 5 = 60.
To simplify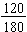 
, rewrite the fraction in a factored form and apply the Fundamental Law of Fractions.
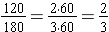
Example: Write the fraction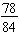 
in simplest terms.
We find the greatest common factor for the numerator and the denominator:
78 = 2 · 3 · 13 and 84 = 22 · 3 · 7 so the GCF(78, 84) = 2 · 3 = 6.
To simplify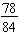 
, rewrite the fraction in a factored form and apply the Fundamental Law of Fractions.
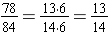
This method is a variation of the previous method where instead of writing the numerator and denominator in a factored form, we divide the numerator and denominator by the greatest common factor.
Example: Find the simplest form for the fraction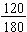 
.
We find the greatest common factor for the numerator and the denominator:
120 = 23 · 3 · 5 and 180 = 22 · 32 · 5 so the GCF(120, 180) = 22 · 3 · 5 = 60.
To simplify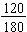 
completely, divide both numerator and denominator by the 60.
Example: Write the fraction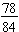 
in simplest terms.
We find the greatest common factor for the numerator and the denominator:
78 = 2 · 3 · 13 and 84 = 22 · 3 · 7 so the GCF(78, 84) = 2 · 3 = 6.
To simplify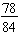 
completely, divide both numerator and denominator by the 6.
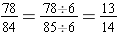
We may use bar diagrams to help solve some types of problems. For example, use a bar diagram to solve the following problem:
Jamie paid Dana three-fourths of the $60 she owed Dana. How much money did Dana receive from Jamie?
A helpful first step in solving a problem of this type is to reword it. With the above example, we are asking the question:
What is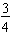
of 60?
A helpful way to solve fraction problems like this problem is to use a bar diagram. A bar is used to represent the whole. So we label it with the amount of the whole.
Since the denominator tells us how many equivalent pieces the whole is divided into, we divide the bar into that many equivalent pieces and label each piece with its value.
Finally, we indicate the required number of fractional parts with a question mark and determine the value represented.
Since one unit is 15, three units would be 45.
So,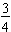 
of 60 is 45.
Dana received $45 from Jamie.
When you work a problem you should show your work as above. We will be building on this method to help better understand multiplication of a fraction and a whole number as well as the multiplication of fractions.
Note that the above problem could be solved by multiplying:
.
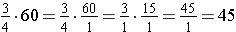Lynn saved $400 and spent $500 of his last paycheck. The ratio of money saved to money spent is 4 to 5, that is, Lynn saved $4 for every $5 spent.
Ratio: Ratios are used to compare quantities. The ratio of a to b can be written either in fraction notation as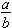 
or as a : b.
The colon notation is specifically reserved for ratios. The fraction form makes sense in many contexts since in some cases a ratio may also be considered as a fraction. For example, in the above problem the ratio of money saved to the value of the paycheck is 4 to 9. We may also consider that four-ninths of the paycheck was saved. The ratio 4:9 conveys the same idea as the fraction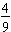 
in this context.
However, the concept of ratio is NOT interchangeable with the concept of fraction. In the above example, the ratio 4:5 does not make sense as a fraction because the amount saved is not a fractional part of the amount spent. Remember that the denominator of a fraction tells how many equal-sized pieces the whole is divided into. Therefore a fraction, by definition, ALWAYS compares to the whole (total). Ratios on the other hand may compare either to the whole or to another part. The above example illustrated each of these two types of ratios: the 4:5 would not make sense as a fraction; whereas, the ratio 4:9 conveys the same idea as a fraction.
Examples: For instance, suppose a class of 30 students has 13 boys and 17 girls.
The fraction of boys must be expressed as a part-to-whole expression. That is, it must compare the number of boys to the total of students (the whole class). The fraction of boys is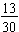 
. And the ratio of boys to the class is 13:30. In this case, the problem may be thought of in terms of either a fraction or a ratio.
The ratio of the class to the boys is a whole-to-part expression. That is, it compares the whole class to the part of the class that is boys. The ratio of the class to boys is 30:13 and may be written as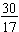 
. But, in this case, it does NOT make sense to think of the whole class as being a fractional part of the boys.
The ratio of boys to girls is a part-to-part expression. That is, it compares the part of the class that is boys to the part of the class that is girls. The ratio of boys to girls is 13:17 and may also be written as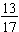 
. But, in this case, it does NOT make sense to think of the boys as being a fractional part of the girls.
.
Notice that the ratio of girls to boys is a different ratio. It is also a part-to-part expression, but it is 17:13 which may also be written as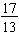 
. Again, it is does NOT make sense to think of the girls as being a fractional part of the boys.
Word problems with ratios and fractions often require us to think carefully about the distinction between a ratio and a fraction. Remember that a fraction MUST compare to the whole.
Example: Forty of the ninety farm animals are cows. The rest are chickens.
This must be a part-to-whole expression. The denominator must be the total number of farm animals. We have the fraction
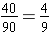
The cows are four-ninths of the farm animals.
Further, the part-to-whole ratio is 4 : 9 (cows to animals). Also, the whole-to-part ratio is 9 : 4 (animals to cows).
This must be a part-to-part expression. The ratio of 40:50 simplifies to 4:5 or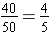 
.
The ratio of cows to chickens is 4 to 5.
Note that the sum of the two values represents the whole, e.g., 40 + 50 = 90 and
4 + 5 = 9. So, the part to whole ratios are 4:9 (cows to animals) and 5:9 (chickens to animals). Also, the whole to part ratios are 9:4 (animals to cows) and 9:5 (animals to chickens).
A man is like a fraction whose numerator is what he is and whose denominator is what he thinks of himself. The larger the denominator the smaller the fraction.
Tolstoy, Count Lev Nikolgevich (1828-1920)
