(a)
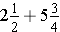
Solution
(b)
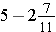
Solution
(c)
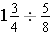
Solution
(d)
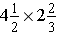
Solution
(e)
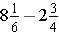
Solution
(f)
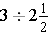
Solution
Fractions - Mixed Operations Practice
The table below summarizes the rules of fraction arithmetic. The first two rows remind us that to add or subtract fractions we need a common denominator. We add or subtract the numerators and keep the common denominator. And as our last step, we simplify.
The third row reminds us that to multiply fractions we need to change any mixed numbers into improper fractions. Then we multiply straight across. And as our last step, we simplify.
The last row reminds us that to divide fractions we also need to change any mixed numbers to improper fractions. Then we multiply the dividend (the first fraction) by the reciprocal of the divisor (the second fraction).
|
Operation |
First Step |
Second Step |
Make Sure |
|
+ |
Find Common |
Add Numerators |
Simplify |
|
– |
Find Common |
Subtract Numerators |
Simplify |
|
Χ |
Change to Improper Fraction |
Multiply Numerators |
Simplify |
|
÷ |
Change to Improper Fraction |
Multiply by |
Simplify |
The following practice problems exemplify some different types of problems, particularly addition or subtraction with regrouping. This is class practice before the lab. Also: Watch the operation. This is mixed practice so you have to pay attention to what operation is written and follow the correct procedure.
|
(a) |
|
Solution |
|
(b) |
|
Solution |
|
(c) |
|
Solution |
|
(d) |
|
Solution |
|
(e) |
|
Solution |
|
(f) |
|
Solution |
"Alice laughed: "There's no use trying," she said; "one can't believe impossible things."
"I daresay you haven't had much practice," said the Queen. "When I was younger, I always did it for half an hour a day. Why, sometimes I've believed as many as six impossible things before breakfast."