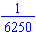(National Weather Service - Lightning Safety).Introduction to Probability
Consider each of the following questions.
Roy Sullivan was struck by lightning seven times. What chance does a person have of being struck by lightning in their lifetime?
How is the insurance premium for car insurance determined for different people?
What is the probability of the Minnesota Vikings winning the flip of the coin at the beginning of a game in all sixteen regular season games?
All three questions are concerned with probability. The probability of a person to have been struck by lightning seven times, as was Roy Sullivan, and survived each of the strikes is quite small on the order of 10–24 (0.000000000000000000000001). Roy Sullivan's probability of being struck by lightning was much greater than most people since he worked as a ranger in Shenandoah National Park most of his adult life (Roy Sullivan - Wikipedia, the free encyclopedia). The National Weather Service estimates the chances of a person being struck by lightning in their lifetime (80 years) are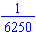 (National Weather Service - Lightning Safety).
Actuaries working for insurance companies use accident data and other factors to determine the risk or probability of a person with certain characteristics of having an accident. The probabilities determined from accident data are a key component in determining a person's insurance rate (Auto insurance risk selection - Wikipedia, the free encyclopedia).
Though the probability of winning the flip of a fair coin is one-half, the probability that the Vikings would win all sixteen regular season flips is only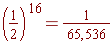
(Coin flipping - Wikipedia, the free encyclopedia).
Probability is the mathematics of chance. Probability is used to describe the predictable long-run patterns of random outcomes. For instance, if you toss a fair coin a single time, the outcome (heads or tails) is completely random and unpredictable. But if a coin is tossed 10,000 times, we would expect that the coin would come up heads approximately half the time.
To start calculating probabilities, we begin with equally likely outcomes. For instance, when tossing a fair coin, a head and a tail are equally likely outcomes. When tossing a standard die each of the six sides is equally likely to show.
When we discuss probability in mathematics, we often perform or study probability experiments. Keeping track of the results from tossing a coin to determine the probability of a single flip would be an example of a probability experiment. Also, a probability experiment could be performed by tossing a standard die or pair of dice.
When we actually perform the experiment to see what happens, we get an experimental probability. For instance, John Kerrich (1903–1985) as a prisoner of war during World War II performed the probability experiment of tossing a coin 10,000 times and recording whether it landed heads or tails. He obtained 5067 heads. So the experimental probability of getting heads for his experiment was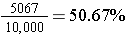 
. Though after 100 tosses, he had obtained only 44 heads. If he had stopped at that point, his experimental probability for a head would have been
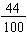or 44%. For more information on John Kerrich or his experiment, see A Brief History of the School of Statistics - University of the Witwatersrand and http://www.wiley.com/college/stat/wild329363/pdf/ch_04.pdf.
Another type of probability that is usable for some types of problems where we do not actually need to perform an experiment is theoretical probability.The theoretical probability of getting heads on a toss of a fair coin is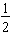 
because there is only one way to get heads out of two equally likely ways for the coin to land. This same type of thinking can be expanded to cover a number of probability situations. But first we need to define some basic terms used in the study of probability.
Sample Space: In probability, the set of all possible outcomes is called the Sample Space. We will use S to represent the sample space. In terms of the language of sets, a sample space is a universal set and an outcome is an element of the universal set.
Example: The sample space for the experiment of toss a coin once would be
S = {H, T} because there are only two possible outcomes, Heads or Tails.
Notice that we frequently abbreviate the outcomes when listing them.
Example: The sample space for the experiment of a toss a standard die would be:
S = {1, 2, 3, 4, 5, 6} because these are the only six possible outcomes.
Event: In probability, an event is a subset of the sample space. In a probability experiment, the event for which we wish to compute the probability is called the target event.
Example: If we want to compute the probability of obtaining a head when tossing a fair coin, then "obtaining a head" is the event. Note that {H} is a subset of S = {H, T}. Also, P(H) represents the probability of obtaining a head.
Example: If we want to compute the probability of getting a 3 or 4 when tossing a standard die, then "getting a 3 or 4" is the target event. Note that E = {3, 4} is a subset of S = {1, 2, 3, 4, 5, 6}. Also, P(E) is the notation that stands for the probability of event E occurring.
For an experiment in which all outcomes are equally likely, the probability of an event E is computed by finding the ratio of the number of elements in the target event E to the number of elements in the sample space S. In the context of probability, we write ratios in their fraction form.
Example: The event of obtaining a 3 or 4 in the experiment of a toss of a standard die is E = {3, 4}. The sample space for the experiment of a toss a standard die is
S = {1, 2, 3, 4, 5, 6}.
So,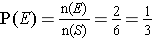 
.
Remember that n(E) is the cardinal number of the set of events and n(S) is the cardinal number of the sample space.
Example: What is the probability of getting an even number when a fair, 6-sided die is rolled? Express this probability as a percent.
First we determine the sample space. Since a fair 6-sided die only has the numbers 1, 2, 3, 4, 5, and 6 as possibilities, and each is as likely to happen as the other, the sample space S = {1, 2, 3, 4, 5, 6} consists of equally likely outcomes.
Then we need to determine the target event set. In this case we want even numbers that can occur on a 6-sided die. Thus our event E = {2, 4, 6}.
So,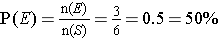 
. The probability of obtaining an even number when a fair standard die is tossed is 50%.
Five names (Dana, Jamie, Lynn, Pat, and Shawn) are put in a hat where one name is to be randomly drawn for a door prize.
What is the sample space?
What is the event where either Dana or Pat's name is drawn?
What is the probability of the event where either Dana or Pat's name is drawn?
Solutions
We can perform several different probability experiments, one after another, and then consider the probability of the series of outcomes that result. For example, we could toss a coin and then toss a standard die. This is a 2-stage experiment because it consists of two separate experiments performed one after the other. Each outcome would also have two parts. Such outcomes are written as ordered pairs using parentheses to indicate that the outcomes must follow in the order they are written. For a two-stage experiment, the sample space is the set of all possible ordered pairs, that is, we form the Cartesian Product of the two stages. For experiments with more than two stages, we often generate the sample space by making a tree diagram. Examples of both of these methods follow.
When there are only two stages in an experiment, a common way to list the possible outcomes is to form a Cartesian Product. This is similar to when you formed sets of ordered pairs in algebra when you graphed on a Cartesian coordinate plane. In algebra, we used a horizontal and vertical axis where the horizontal axis represented the first values, x, and the vertical axis represented the second values, y, in ordered pairs, (x, y). Here, we create a table to aid us in forming the Cartesian Product where the rows represent the possible outcomes for the first experiment (down the side) and the columns represent the possible outcomes for the second experiment (across the top). Like this:
To form the Cartesian Product, we list in each interior cell of the table, the ordered pair that results from the outcome listed at the side followed by the outcomes listed at the top.
The sample space is the set of outcomes listed in the shaded cells,
S = {(H,1), (H,2), (H,3), (H,4), (H,5), (H,6), (T,1), (T, 2), (T,3), (T,4), (T,5), (T,6)}.
Note that we have twelve possible outcomes in this sample space for this two-stage experiment, which follows from the Fundamental Principle of Counting 2 · 6 = 12..
When a probability experiment involves more than two actions, we often use a tree diagram to find the sample space. For example, for the experiment "toss a coin three times and record the results from each toss", we could draw the following tree diagram.
The sample space for the problem is S = {(H,H,H), (H,H,T), (H,T,H), (H,T,T), (T,H,H), (T,H,T), (T,T,H), (T,T,T)}. Each outcome is an ordered triple and we usually write the set in the abbreviated form S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}. Also, note that HHT, HTH, and THH are three distinct outcomes even though they both consist of two heads and one tail. Also, note that there are 2 · 2 · 2 = 8 outcomes, which follows from the Fundamental Principle of Counting.
A boy and girl are to be randomly chosen to represent their class. The boy is chosen from Tom, Dick, and Harry. The girl is chosen from Jane, Kathy, Pam, and Sally. Find the sample space for this problem.
Solution
Sometimes the outcomes in a probability experiment are not equally likely. For instance, in the spinner below, the outcomes blue and yellow are equally likely because they represent the same area on the spinner, but the outcome red is twice as likely because it occupies twice as much area as either blue or yellow. The sample space is S = {blue, red, yellow} even though each outcome is not equally likely.
But to simplify the problem for this case, we could rewrite the sample space as {blue, red1, red2, yellow}. By doing this, each of the outcomes listed is equally likely because we have listed the color red twice. Notice that because we were writing this as a set, we cannot simply write red in the set twice, because each element in a set must be distinct or it would represent the same element. By listing the outcomes as red1 and red2, we are indicating that there are two distinct areas that result in the outcome of red as illustrated in the diagram below.
Note: Often a sample space does not have its outcomes all equally-likely. Further, we are often not able to do the above procedure where the outcomes are made equally-likely.
He who has heard the same thing told by 12,000 eye-witnesses has only 12,000 probabilities, which are equal to one strong probability, which is far from certain.
Voltaire (1694-1778)In J. R. Newman (ed.) The World of Mathematics, New York: Simon and Schuster, 1956.