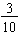and 
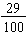.Comparing Decimals and Operations with Decimals
Decimal Order, Addtion, and Subtraction
Solve the following problem.
Compare the cost of electricity for two local electric co-ops. Wild Rice Co-op charges 0.094 dollars per kilowatt-hour with a surcharge of 0.008 dollars per kilowatt-hour. Cattail Lake Co-op charges 0.0959 dollars per kilowatt-hour with a surcharge of 0.0052 dollars per kilowatt-hour.
The problem involves the addition of decimals and the comparison of decimals since the total charge per kilowatt-hour needs to be determined for each co-operative before the values are compared. When we make the comparisons, we need to be very careful that we are comparing their place-values and not the number of nonzero digits. For example, if we compare the surcharges, we note the 0.008 (eight thousandths) is more than 0.005 (five thousandths). So, we would conclude that 0.008 > 0.0052. We would not compare the 8 and 52, which would have given us an incorrect solution since 52 > 8.
We note that without the surcharge Wild Rice Co-op has a lower cost per kwh since 0.094 < 0.0959, but the surcharge for Cattail Lake Co-op is less since 0.0052 < 0.008. By adding the charge and surcharge, we find that the cost per kwh for Wild Rice Co-op is 0.102 dollars per kwh and for Cattail Lake Co-op is 0.1011 dollars per kwh. The cost of electricity for Cattail Lake Co-op is less than that of Wild Rice Co-op since 0.1011 < 0.102. If we subtract their costs, we find that the cost for Cattail Lake Co-op is 0.0009 dollars per kwh hour less than that of Wild Rice Co-op.
This problem motivates the importance of place value when comparing decimals. It also motivates the use of place value for lining up the decimal points in the addition and subtraction of decimals.
When we compared and ordered fractions, we needed to find a common denominator. One of the advantages of using the decimal form of fractions is how much simpler it is to find common denominators.
Example: Compare 0.3 and 0.29.
First, note that we are not comparing 3 and 29; we must consider the place-values of the 3 and 29. By use of place-value and writing 0.3 and 0.29 as common fractions, we see that we are comparing 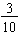and .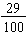
But we can simplify this process by noting that these fractions have a common denominator simply by realizing 0.3 = 0.30. Extending decimal representations until they have the same number of decimal places automatically gives us common denominators.
So, to compare 0.30 to 0.29, we compare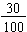 
and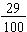 
.
Since 
, we conclude that 0.3 > 0.29.
The above example shows that we can compare terminating decimals by writing them with the same number of decimal positions; this is the same as finding a common denominator.
Example: Order the list 0.8, 0.123, 0.045, 0.03 from the least value to the greatest value.
We first rewrite the list as decimals with a common denominator, that is, we write each of the decimals in terms of thousandths: 0.800, 0.123, 0.045, 0.030. We now have
0.030 < 0.045 < 0.123 < 0.800.
By rewriting them in the original form, we conclude that
0.03 < 0.045 < 0.123 < 0.8.
If we are comparing both terminating and repeating decimals, we would want to write out enough repeating position to make the comparison clear.
Example: Order the list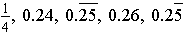 
from the least value to the greatest value.
We first rewrite each in decimal from with the same number of decimal positions:
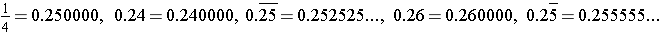
We then have that 0.240000 < 0.250000 < 0.252525… < 0.255555… < 0.260000.
We conclude that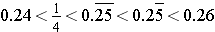 
.
A class of students at Hogwarts were comparing the lengths of their wands. Harry's wand was 2.4 decimeters long, Hermione's was 2.435 decimeters long, Ron's was 2.371 decimeters long, and Malfoy's was 2.39 decimeters long. Rank them from who had the longest to who had the shortest wand.
Solution
We rewrite decimals in expanded common fraction form to justify the "line up decimal points" for the addition of decimals. The decimal expanded notation helps us see how place value with decimal addition is important.
Example: Find the sum 4.8 + 5.24.
First note that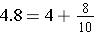 
and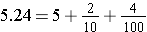 
.
We add these two values by place-value
The addition of the fractions with common denominators justifies that lining up the decimal points to add fractions is just the addition of the corresponding place-value. Below, we complete the problem without changing to common fractions.
With common denominators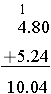 
, which justifies line up decimal points 
.
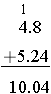Yesterday, we received 1.3 inches of rain and today we received 1.83 inches of rain. How much rain did we receive over the two days?
Solution
When we added whole numbers, we right-justified the values and added down the columns. Lining up the last digit in each addend put all the digits with the same place value in the same column.
Now that we have extended the place value system to include decimal fractions, we can no longer line up the last digit in order to line up the place values, because the last digit of the decimals does not necessarily have the same place value the way it was with whole numbers.
Instead, we need to line up the decimal points to line up the corresponding place values, regardless of how many decimal places an addend has.
Example: Find the sum 4.5 + 34.98 + 6.
For the numerals to line up with the correct place value, we write the problem as
Notice that the 6 is six ones, and therefore can be written as 6. Also, we can fill in the end decimal places with zeros if we want to make all of the addends have a value in each place value position. This is not necessary, but sometimes it helps us to keep the place values lined up properly.
Just as with adding whole numbers, when a group of 10 is collected in one place value, that group of ten is recorded as 1 in the next place value to the left.
The sum 4.5 + 34.98 + 6 is 45.48.
Shawn's daily water useage over three days was 5.7 cubic feet, 12 cubic feet, and 9.35 cubic feet. How much water did Shawn use over the three days.
Solution
Subtraction of decimals works in a similar way to addition. We line up the decimal points in order to line up the place values. Regrouping works just as it did with whole numbers, since each place value is still ten times as much as the place value on its right.
Example: Find the difference 400.5 – 37.25.
The difference 400.5 – 37.25 is 363.25.
Here is a modification of the above standard subtraction algorithm that simplifies the exchanges.
A gas tank contains 13.2 gallons of gas at the beginning of a trip and 5.37 gallons at the end fo the trip. How many gallons of gas were used on the trip?
Solution
"Repeating decimals do not end," remarked Dana in his infinite wisdom.