Laws of Exponents
Scientific Notation
If you have ever taken a Chemistry class, you may have encountered the following numbers:
There are approximately 602,214,179,300,000,000,000,000 molecules in one mole of any substance (this quantity is called Avogadro's number).
Avogadro constant - Wikipedia, the free encyclopedia
The mass of an electron is approximately 0.0000000000000000000000000009109382 grams.
Electron rest mass - Wikipedia, the free encyclopedia
Notice these two values are inconvenient to write in regular decimal notation because there are so many digits to write. When values are very large or very small it is often more manageable to write the numerals using scientific notation. Scientific notation - Wikipedia, the free encyclopedia
Scientific notation is a representation that uses a decimal number times a power of ten. The decimal value is usually written with one digit, not zero, in front of the decimal point, and when multiplied together with a power of 10, the scientific notation exactly equals the value it represents. This is referred to as the normalized form for scientific notation.
Before when we studied scientific notation (Session 13), we only worked with whole numbers. This meant that we allowed more than one non-zero digit and all of the powers of 10 were positive powers. Now we extend that notation to include any decimal fraction.
We write the mass of an electron (given above) in scientific notation. First, when changing to scientific notation, we move the decimal point until the first non-zero digit in the numeral is in front of the decimal point. Then the power of ten represents the number of place values the decimal point is moved.
Example:
So, in scientific notation, the mass of an electron in grams is approximately 9.109382 × 10–28.
Notice that 10–28 = 0.0000000000000000000000000001 and if we multiply that by 9.109382 the result is 0.0000000000000000000000000009109382, which is the decimal value with which we started.
When trying to remember whether to use a positive or a negative exponent, or whether to move the decimal point right or left, it is much better to think about the meaning of the multiplication involved in the scientific notation. Multiplying by a positive power of 10 makes the number larger and multiplying by a negative power of 10 makes the number smaller.
4.56 × 105 makes the 4.56 greater in value by 5 place values so it equals 456,000.
1.2 × 10–4 makes the 1.2 less in value by 4 place values so it equals 0.00012.
Likewise, to write a number that is greater than one in scientific notation, the power of 10 will be positive (or possibly zero), and to write a number less than one in scientific notation, the power of 10 will be negative.
Formal Definition: To express a number in scientific notation (normalized form), we write it in the form a × 10k , where a is a decimal with 1 ≤ a < 10 and k is an integer.
Example: In scientific notation, Avogadro's number is approximately 6.022141793 × 1023.
Matching this with the formal definition, a is the decimal 6.022141793 and k is the exponent 23.
If we multiply this out, the positive twenty-third power moves the decimal point 23 place values right, making the decimal part of the number larger by that many place values.
This is exactly equal to the original value of 602,214,179,300,000,000,000,000.
|
Standard Numeral |
Verbal Form |
Scientific Notation |
|
5,400,000,000 |
Solution |
Solution |
|
Solution |
six hundred thirty-one million |
Solution |
|
Solution |
seventy-one ten-thousandths |
Solution |
|
0.0000012 |
Solution |
Solution |
|
Solution |
Solution |
1.7 × 1010 |
Setup and compute the solution to the following problems using exponents.
Billy and Betty are each flipping one coin. Billy flips his three times and Betty flips hers four times. How many possible outcomes are there for Billy? How many possible outcomes are there for Betty? If we consider this all one experiment in which Billy does his part first and then Betty does her part, how many possible outcomes are there altogether?
We know that the number of possible outcomes for Billy is 23 = 8 and the number of possible outcomes for Betty is 24 = 16.
The total number of outcomes for both is 27 = 128. Note that 23 × 24 = 8 × 16 = 128 = 27.
Find the volume using scientific notation.
An astronomer studying a region of space needs to determine the volume of a cubic region whose edges measure 3 × 108 miles long. Find the volume of that region of space.
To find the volume of a cube, we need to cube the length of an edge. For this problem, we would have to compute (3 × 108)3. How can we compute this problem by leaving it in scientific notation? We will solve this problem later in the session after we have formed the necessary properties.
The above two problems motivate the need for properties of exponents to aid in computation. We begin to develop some of the basic properties of exponents. Later in the course, we will extend these properties and develop more properties.
We previously (Session 13) multiplied terms like x2 · x3 and 3y2 · 7y by applying the definition of exponent.
Example:
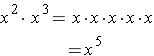
In this case we see that is the base for each of the exponent expressions being multiplied and that we end up with x being used as a factor a total of 2 + 3 = 5 times.
Example:

In this case we see that y is the base for each exponent expression being multiplied and that we end up with y being used as a factor a total of 2 + 1 = 3 times.
Now we develop rules that make these computations shorter and more efficient.
The previous examples above show what happens when we multiply two exponential expressions that have the same base. The fact that the base number is the same allows us to simply sum the number of times the base is used as a factor. It is important to remember that this only happens when the bases are the same.
Two More Motivation Examples:

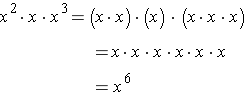
Note that a value with no exponent is the same as having an exponent of one. For example, 51 = 5 and x1 = x.
Now we are ready to formalize what we know about how to multiply variable expressions that have the same base. We see from the examples above that when we multiply exponent expressions that have the same base, we get that base as many times as the sum of the exponents of the base.
Multiplication of Values with the Same Base. When multiplying two exponential expressions with the same base, the product has the same base with an exponent that is the sum of the exponents of the factors.
General Property: bm · bn = b (m + n)
Examples: 1019 · 1023 = 1019+23 = 1042 37 · 38 = 37+8 = 315
y 4 · y 5 = y 4+5 = y 9 57 · 5 · 56 = 57+1+6 = 514
Examples with coefficients or more than one variable:
|
|
|
Simplify each expression in terms of the exponents.
|
107 · 1014 |
Solution |
|
m4 · m5 |
Solution |
|
7ab2 · 9a3b7 |
Solution |
Two Motivation Examples:
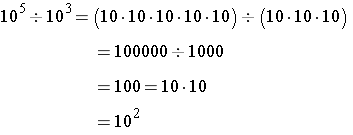 or
or
 or
or
Note that the exponent in the quotient is the difference between the exponents in the dividend and divisor.
Division of Values with the Same Base. When dividing two exponential expressions with the same base, the quotient has the same base with an exponent that is the difference between the exponents of the dividend and divisor.
General Property: bm ÷ bn = b (m – n) or 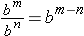 where m ≥ n and b ≠ 0.
where m ≥ n and b ≠ 0.
(In Session 41, we will extend this property to values with m < n.)
Examples: 1023 ÷ 1019 = 1023–19 = 104 38 ÷ 37 = 38–7 = 31 = 3
y 9 ÷ y 3 = y 9–3 = y 6 58 ÷ 56 = 58–6 = 52
Since we are only using whole numbers at this time, we require that the first term have an exponent of greater value that the second term. This property will be generalized later in the course after we have introduced integers.
Simplify each expression in terms of the exponents.
|
|
Solution |
|
|
Solution |
|
|
Solution |
Two Motivation Examples that Use the Division Property:
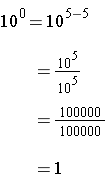
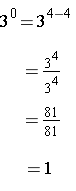
Note the result is always one.
Exponent of Zero. When a nonzero value is raised to the zero power, the result is one.
General Property: a 0 = 1, when a ≠ 0. (Note that division by zero is undefined.)
Examples: 70 = 1
80 = 1
(xy)0 = 1 provided x ≠ 0 and y ≠ 0
Likewise, we have previously been simplifying variable expressions like (3x)2 and (2x2y)3 by applying the definition of exponent.
.Example:

In this case we see that when the product (3x) is raised to the second power, it comes out the same as a raising each factor to the second power.
Example:

In this case we see that when the product (2x2y) is raised to the third power, it is the same as raising each factor to the third power.
Two Basic Examples using the Rule for Multiplication with the Same Base:
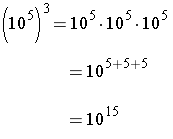
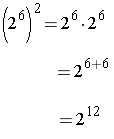
Note that the exponent in the result is the product of the exponents in the original expression.
Raising an Exponential Expression to a Power. When an exponential expression is raised to a power, the result has the same base with an exponent that is the product of the exponents.
General Property: (bm)n = bmn
Examples: (103)9 = 103(9) = 1027
(38)7 = 38(7) = 356
(y 9)3 = y 9(3) = y 27
(58)6 = 58(6) = 548
Simplify in terms of the exponents
|
(107)8 |
Solution |
|
(d9)6 |
Solution |
Two Motivation Examples:
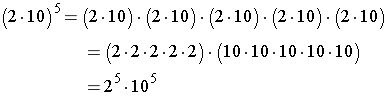
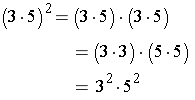
Note that the commutative and associative properties were used to rearrange the factors. Further, note that the result has the same exponent on both terms as in the original expression.
Power of a Product. When product of two factors is raised to a power, the result is a product with the two factors each having the same exponent that was the power the expression was raised to.
General Property: (ab)m = ambm
Examples: (7 · 10)9 = 79 · 109
(3 · 8)7 = 37 · 87
(xy)3 = x3y3
(ab)4 = a4b4
Examples using more than one law or property of exponents:
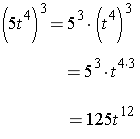

Simplify in terms of the exponents
|
(4 · 10)3 |
Solution |
|
(3a)4 |
Solution |
|
(2x2y3)5 |
Solution |
We are now able to answer the astronomer's problem given on page 2 of this session.
An astronomer studying a region of space needs to determine the volume of a cubic region whose edges measure 3 × 108 miles long. Find the volume of that region of space.

The cubic region of space has a volume of 2.7 × 1025 cubic miles.
Use the Laws of Exponents to simplify the expression (2a6b)3(3a2b3)2.
Solution
To multiply a pair of numbers given in scientific notation, we can use the Commutative and Associative Properties of Multiplication to group the decimal values together and the powers of 10 together. We also use the exponent rule for multiplying exponential expressions that have the same base, bm · bn = b (m+n).
Example: Find the product (9 × 103)(5 × 102), using scientific notation.
Solution: First, grouping the decimal parts and the powers of 10 together, we get:

This is not quite the usual way we express a number in scientific notation because there are two non-zero digits in front of the decimal point, so we can rewrite the 45 part in scientific notation as 4.5 × 101 which gives us a final answer of

Note that this is called the normalized form for scientific notation. We will write our solutions in the normalized form, with only one digit (not zero) in front of the decimal point. For now, we are restricted to doing multiplication using positive powers, since we have not yet studied integer arithmetic.
Approximately, how far would a photon travel in one year? A year is approximagely 3.15 × 107 seconds. Light travels at approximately 3 × 108 meters per second. Photon - Wikipedia, the free encyclopedia
Solution
Adding and subtracting with scientific notation may require more care, because the rule for adding and subtracting exponential expressions is that the expressions must havelike terms. Remember that to be like terms, two expressions must have exactly the same base numbers to exactly the same powers. Thinking about decimal arithmetic, the requirement that we have the same powers makes sense, because that guarantees that all of the place values are lined up properly.
Example: (4.5 × 104) + (1.75 × 104) can be completed using the distributive property of multiplication over addition, i.e., factor out the common factor 104.
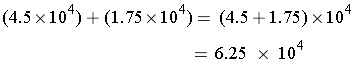
We run into trouble, though, with problems like (7.5 × 103) + (5.25 × 105) because the powers of 10 differ, so we need to modify the problem before we factor. We work around this by using our exponent property bm · bn = b (m+n) to rewrite the 105 as 102 · 103 and then grouping the 102 with the 5.25.

We see that this solution is not in standard scientific notation form because the decimal part has more than one digit in front of the decimal point. So we have one more step to finish the problem. We need to rewrite 532.5 as 5.325 × 102 and then simplify the powers of ten.
Continue from above:

Subtraction can be done the same way as addition, by getting the powers of ten to match; factoring out the power of ten that is the same, and subtracting the decimal values that come together when the power of ten is factored out. Then we simplify if the answer is not in normalized form.
Approximately, how much further from the sun is Saturn than Earth. Earth is approximately 9.3 × 107 miles from the sun and Saturn is approximately 8.87 × 108 miles from the sun.
Solution
Several scientists were all posed the following question: "What is 2 times 2?"
The engineer whips out his slide rule (so it's old) and shuffles it back and forth, and finally announces "3.99".
The physicist consults his technical references, sets up the problem on his computer, and announces "it lies between 3.98 and 4.02".
The mathematician cogitates for a while, then announces: "I don't know what the answer is, but I can tell you, an answer exists!".
Philosopher smiles: "But what do you mean by 2 times 2?"
Logician replies: "Please define 2 times 2 more precisely."
The sociologist: "I don't know, but is was nice talking about it".
Behavioral Ecologist: "A polygamous mating system".
Medical Student: "Four". All others looking astonished ask "How did you know??" Medical Student: "I memorized it."