Review of Ratio Concepts
Ratios and Proportions
How would you solve the following problem?
The ratio of girls to boys in the chess club is a 2 to 1. If there are 10 boys in the chess club, how many girls are there in the club?
Here is one possible way we could reason out the problem. We are told that the ratio of girls to boys is 2 to 1. This ratio must be interpreted as 2 girls to 1 boy because of the order of the words describing the ratio. We draw a diagram of the situation by drawing 2 girls for every 1 boy until we have drawn a total of 10 boys. Let's use B for boy and G for girl. Then our diagram would look like this:
We see from the diagram that when there are 10 boys, there are 20 girls.
Another way to work the problem would be to reason it out by thinking that there are two girls for every one boy (since the ratio of girls to boys is 2 to 1). So, each boy would be paired with two girls. And since we have ten boys each paired with two girls, there must be ten groups of two girls, 10 · 2 = 20. We would conclude that there are 20 girls in the club.
Ratio problems of this type are common where we desire to find an unknown quantity when we know the ratio between it and a known quantity. Some common problem examples would be scaling up or down recipes, mixtures, maps, or architectural drawings.
Though the above problem was not too difficult to reason out, we would like to develop some general methods that would help with more complex problems. Problems of this type are often solved using proportions, which we will introduce later in this lesson.
A recipe calls for three cups of flour for each cup of sugar. How many cups of flour are needed if five cups of sugar are used?
Solution
See the previous Session 19 for an introduction to ratios.
Definition: A ratio is a comparison of the relative size of two numerical quantities. A ratio comparing quantity a to quantity b is usually written as a : b or in fraction form as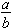 
and read verbally as the phrase "a to b."
Simplest Form: When writing a ratio, we will usually write it in simplest form. That is, we will simplify it so that the quantities involved have a greatest common factor of one.
Example: A garden is 20 feet long and 8 feet wide. Express the ratio of the length of the garden to the width of the garden in simplest form.
Order Matters: In a ratio, order is important. That is, the ratio a : b is not the same as the ratio b : a. A ratio compares two quantities in the order the items being quantified are listed.
Example: A small college has 35 faculty members and 1,000 students. Express the student to faculty ratio in simplest form.
The student to faculty ratio is 200 to 7, which is different than faculty to student ratio of 7 to 200. Since we were asked for the student to faculty ratio, the number of students must be listed in the numerator of the fraction form and as the first value in the colon notation.
A ratio gives us a nice way to compare the size of two quantities. If we are given two quantities, we can find the ratio of one to the other. Similarly, if we are given a ratio along with one of the original quantities, we can work backwards to find the second original quantity, as we did in the motivation problem with the chess club.
Example: Pat used three gallons of gas to drive seventy miles. If Pat used twelve gallons of gas, approximately how many miles could Pat drive?
The ratio of gallons of gas used to distance driven is 3 to 70. Since Pat used 12 gallons and 3(4) = 12, we could work the problem like we did with equivalent fractions. So, the ratio of 3 to 70 would be equivalent to the ratio of 3(4) to 70(4) or in other words 12 to 280. We conclude that Pat could drive 280 miles on 12 gallons of gas.
This problem leads to the concept of proportions, which is the equivalence of two ratios.
The full-time faculty to student ratio at MSUM is 1 to 23. If there are 325 full-time faculty members, approximately how many students are there?
Solution
Ratio problems are often solved by using proportions. A proportion is an equation formed with two ratios that are equal. One method for solving a proportion problem is to find the appropriate equivalent ratio. We could have solved the original problem by setting up a proportion and then finding what the equivalent fraction would have to be.
Example: The ratio of girls to boys in the chess club is a 2 to 1. If there are 10 boys in the chess club, how many girls are there in the club?
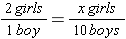
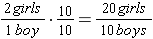
So when there are 10 boys, there must be 20 girls. Note that we wrote the ratios in the proportion in the fraction form and that the second ratio must be in the same order as the first ratio. In this case the numerals representing the number of girls are in the numerators and the numerals representing the number of boys are in the denominators.
Example: A student attends only 3 out of every 4 days during a summer course. If the student attended 15 days, how many days did the summer course run?
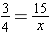
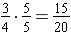
Note that this time the missing value is in the denominator, since the denominator in the first ratio is days attended to total days.
The summer school course was 20 days long.
Be Careful with the Wording: We need to watch the wording carefully when working any ratio or proportion problem.
Example: A state lottery sells scratch tickets and guarantees that one out of every six tickets is a winning ticket.
(a) Express the ratio of winning tickets to losing tickets in simplest form.
Be careful. The ratio of winning tickets to losing tickets is not 1 : 6. The correct ratio is 1 : 5, since on average out of six tickets we would expect one winning ticket and five losing tickets.
(b) How many tickets would you expect to have to buy in order for three of them to be winners?
Since we are looking for the total tickets, we use the ratio of the winning tickets to the total number of tickets, which is 1 : 6. The proportion for the problem would then be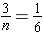 
, since we desire three winning tickets but do not know the expected total. We solve the problem using equivalent ratios
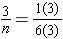
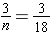
To obtain three winning tickets, we would expect to have to buy about 18 tickets. In practice, if we were to actually buy 18 tickets, we may not actually get exactly 3 winning tickets, since this is actually a probability question where the number of tickets could be more or less than 18 tickets, but the average expected number would be 18.
If a beverage company advertices one of every eight bottles of pop wins a free bottle of pop, how many winning bottles would one expect in a gross?
Solution
A mother of three is pregnant with her fourth child.
One evening, the eldest daughter says to her dad: "Dad, do you know what I just found out?"
"No."
"The new baby will be Chinese!"
"What?!"
"Yes. I just read in the paper that statistics shows that every fourth child born nowadays is Chinese."