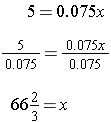
The Percent Equation
Solving Percentage Problems
Solve the following percentage problem.
A pair of boots at a local Fargo-Moorhead chain store is $195. How much more would the boots cost if you buy the boots in the Fargo store than they would cost in the Moorhead store? The sales tax rate in Fargo is 7% and Moorhead has no sales tax on clothing.
The boots would cost 7% more in Fargo than in Moorhead due to the sales tax. By the definition of percent, the rate of 7% would mean that a person would pay 7¢ for every 100¢; that is, $0.07 for each $1. Since the price of the boots is $195 and each dollar contributes $0.07 of tax, a person would need to pay $0.07(195) = $13.65 additional for sales tax. The boots would cost $13.65 more in Fargo than in Moorhead.
This problem illustrates an example showing how understanding percentages can save someone money when shopping for a better deal. Often people just look at the price of an item and do not factor in all the costs. For example, a clothing item could be listed at a lower price in Fargo, yet actually be cheaper in Moorhead. In this session, we introduce methods for solving problems involving percentages.
Reminder: A percent is a ratio that compares numerical quantities in terms of the number of parts out of 100.
In the previous session, we translated among the percent, decimal, and fractional forms of a value. In this session, we take a percentage of a given quantity and solve problems involving percents.
The basic approach we use is to translate the problem into an equation and then solve the equation. It is often helpful to first restate the problem into an abbreviated form before translating the problem to an equation form. Key words are often helpful in the restatement and translation steps. For many of these percentage problems the verb "is" translates as "equals" and the preposition "of" translates as the operation of multiplication, "times".
An example of translating a percent problem and then solving it would be:
Example: Dexter (the Kaputian monkey) steals the keys from Larry the watchman at the Museum of Natural History 46% of the nights. In the last 50 nights, how many nights has Dexter stolen the keys?
First clue: The missing number is the number of nights that Dexter has stolen the keys. We assign a variable to this missing value: Let x represent the number of nights Dexter stole the keys.
Restate: 46% of the last 50 nights is the number of times Dexter has stolen the keys.
Translate: 0.46 (50) = x Note 46% = 0.46, of is times, is is equals, and x is the number of nights the keys were stolen.
Solve: x = 0.46(50) = 23
Answer: Dexter has stolen the keys 23 nights out of the last 50 nights.
Check: Does this sentence make sense in terms of the original problem?
Yes, we would expect the number of nights he stole the keys should be less than 50. Also, the ratio 23 to 50 is equivalent to the ratio 46 to 100 (or 46%).
Example: The figures from the diorama room are only 7.5% of the height of the people they represent. Approximately, how tall was Octavius if his diorama figure is only 5 inches tall? Augustus - Wikipedia, the free encyclopedia
First clue: The missing number is the height of the real Octavius. Let x represent the height of the real Octavius (in inches).
Restate: The 5-inch tall diorama figure is 7.5% of the height of the real Octavius.
Translate: 5 = 0.07(x) Note is is equals , 7.5% = 0.075, of is times, and x is the height of the real Octavius.
Solve: Since we need to solve this equation, we use our properties of equality as we have before.
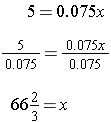
Answer: The original Octavius was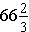 
inches tall, which is approximately 5 feet 7 inches.
The problem many people have with this technique is being able to restate the problem clearly as a percent relationship. We further explain the three basic parts of a percent relationship in the rest of the lesson.
You correctly answered questions worth sixty-eight points on a test that was 80% of the total points possible. How many total points were possible?
Solution
As you read the examples, ask yourself if you understand how to restate each problem as a simple percent relationship.
In this equation, the base is the number of which we are taking a percentage and the amount is the value that results from taking the percent of the base. This means that in any percent problem, there are three basic values to be concerned about: the percent, the base, and the resulting amount. A percentage problem may ask us to find any one of these three values.
The Basic Percent Equation is the basic relationship that we need to learn to understand. We need to know how to identify which number is the base and which number is the amount?
Example: Suppose you go out to dinner at a restaurant. After dinner when you pay your bill, you decide to give your server a 15% tip. If the total bill (before tipping) is $20.00, then how much should you leave as a tip?
We can restate the problem as: 15% of the total bill of $20 is the tip.
The base in this case is the total bill of $20.00, since this is the value we are taking a percentage of. We solve for the tip which is the resulting amount.
(percent) × (base) = (amount)
(percent) × (bill) = (tip)
(15%) × ($20) = x
where x represents the amount of the tip.
Next, we convert the percent to either fraction or decimal form and then multiply:
x = (0.15)(20)
x = 3
You would tip the server $3.
Example: You live in a city that charges 6% sales tax on all purchases. If you go to a store and purchase $30 worth of merchandise, what is your total bill?
We can restate the sales tax portion of the problem as: 6% of the $30 worth of merchandise is the sales tax.
Next, we compute the tax on the purchase using the Basic Percent Equation. We do not know the amount of sales tax, so we let x represent the amount of sales tax in the equation and solve for x.
(percent) × (base) = (amount)
(6%) × ($30) = (amount of tax)
We compute
(0.06)(30) = x
1.80 = x
The amount of tax is $1.80. Notice that this does not give the total bill. It only gives the amount of tax paid on the purchase. To compute the total bill, we add the amount of tax on to the cost of the merchandise.
Since $30.00 + $1.80 = $31.80, the total bill is $31.80.
We may also solve the problem in a single equation.
Second Method for the above problem: You live in a city that charges 6% sales tax on all purchases. If you go to a store and purchase $30 worth of merchandise, what is your total bill?
Note that you will pay 100% of the cost plus 6% for sales tax, so you will pay 106% of the cost of the merchandise.
We restate the problem as: 106% of the $30 worth of merchandise is the total cost.
Next, we compute the tax on the purchase using the Basic Percent Equation. We do not know the total cost, so we let x represent the amount of the total cost in the equation and solve for x.
(percent) × (base) = (amount)
(106%) × ($30) = (amount of the total cost)
We compute
(1.06)(30) = x
31.80 = x
The total bill is $31.80.
For the next examples, formulate each part for yourself before checking.
Example: Suppose that you take a quiz and get 15 correct out of 20. What is your percent score on the quiz?
We restate the problem as: restate
Again, we will use the variable x for the unknown percent.
Translating into the Basic Percent Equation: (percent) × (base) = (amount). translate
Solve the equation: solve
At this point, we have several choices for changing the result to a percent. Here are two ways: Two Methods
We now have the solution. answer
Example: Suppose that you work in the quality control department of a factory. During one afternoon, you check 80 components and find that 12 of them are defective. What percent of the components that you checked were functioning properly?
We restate the problem as: restate
Again, we work this problem using our Basic Percent Equation. We are looking for the percent, so we use x for the percent value in the equation. Since the base is what we are taking the percent of, the base in this situation would be the 80 components that were checked. We want to know what percent of the 80 components worked properly. Since 12 of the components were defective, we note that the number of parts that work properly is 80 – 12 = 68.
Using the Basic Percent Equation we get: translate
Solving the equation we get: solve
We now have the solution. answer
Example: In a recent survey, 75% of the people surveyed were concerned about the economy. If 60 of the people surveyed were concerned about the economy, how many people took part in the survey?
Restate
Translate
Solve
Answer
A store owner wants to make a 30% profit based on the owner's cost. If the owner made a profit of $18, what was the cost of the item for the owner?
Solution
Mathematics is made of 50 percent formulas, 50 percent proofs, and 50 percent imagination.