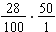must have the same answer as 
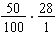since 
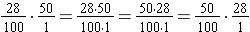. More Percent Problems
Mental Short Cuts
Mentally Compute the Solution to the Following Problem
A restaurant bill is $48. If a person leaves a 15% tip, how much should the person tip?
Since 15% is 10% plus 5% and 5% is half of 10%, we could first take 10% of $48 and then add half as much. Since 10% is the same as one-tenth, one-tenth of $48 is $4.80. We only needed to move the decimal point one place value position. One-half of $4.80 is $2.40. Since 4.80 + 2.40 = 7.20, the person should leave a tip of about $7.20.
This problem motivates the use of compatible values to more easily compute solutions to percent problems mentally. In this session, we consider shortcuts to computing percent problems some of which lead to mental shortcuts.
The word "of" in mathematics often means to multiply. This makes problems like "find 10% of 250" easy to translate directly into the multiplication problem (0.10) · (250). We can immediately write and work the necessary multiplication problem without using an equation.
(250)(0.10) = (250)(0.1) = 25.0 = 25
Notice that we needed both the percent value and the base value in order to use this shortcut of the Basic Percent Equation, (percent) × (base) = (amount).
A 30% off coupon is used to purchase a shirt priced at $65. How much will a person save by using the coupon?
Solution
By now, you have probably recognized that some percents are equivalent fractions with which we are very familiar. When these percents occur with "compatible numbers" (numbers that simplify or multiply easily), we may calculate the percent problems mentally.
Example: 100% is the whole, so 100% of 782 is 782 since 1(782) = 782.
Example: 50% is one-half, so 50% of 84 is 42 since ½ (84) = 42.
Example: 25% is one-fourth, so 25% of 20 is 5 since ¼ (20) = 5.
Example: 10% is one-tenth (one place value less), so 10% of 36.5 is 3.65 since 0.1(36.5) = 3.65.
The shortcut is even more useful by realizing that due to the Commutative Property of Multiplication, "28% of 50" must have the same final answer as "50% of 28".
This is due to the fact that the multiplication 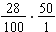must have the same answer as 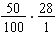since .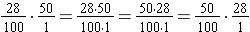
So 100%, 50%, 25,% and 10% are not only easy percents to use when the numbers are compatible; they are also easy bases to take a percentage of, since 40% of 25 must have the same value as 25% of 40 (solution). These are not the same problem, but they have the same arithmetic answer. Since when we multiply the fraction forms, we can use the commutative property in the numerator and the arithmetic becomes identical.
Note: Here are some basic percent-fraction equivalences that should be memorized for use with mental estimation and compatible numbers.
Work these problems mentally.
Sandy has a credit card balance of $960. If the interest rate is 12½%, how much interest would Sandy owe?
Solution
Jamie has a $50,000 CD in Lake Region Bank. The APR (annual percentage rate) is 2.8%. How much interest will Jamie receive at the end of one year?
Solution
Three percent exceeds 2 percent by 50 percent, not by 1 percent.
Work Joke Professional Jokes