1.1.2 Examples of Axiomatic Systems  Printout
Example is not the main thing in influencing others, it is the only thing.
—Albert Schweitzer (1875–1965)

        This example is written to develop an understanding of the terms and concepts described in section 1.1.1 Introduction to Axiomatic Systems.

Example 1. Consider the following axiom set.

Axiom 1.  Every ant has at least two paths.
Axiom 2.  Every path has at least two ants.
Axiom 3.  There exists at least one ant.

1. What are the undefined terms in this axiom set?
   The undefined terms are ant, path, and has. Note that ant and path are elements, and has is a relation since it indicates some relationship between ant and path.

2. Prove Theorem 1. There exists at least one path.
   Note that Axiom 3 guarantees the existence of an ant, but no axiom explicitly states that there is a path. We need to prove the theorem to prove the existence of a path.
   Proof.  By Axiom 3, there exists an ant. Now since each ant must have at least two paths by Axiom 1, there exists at least one path. //

3. What is the minimum number of paths? Prove.
   The minimum number of paths is two.
   Proof.  By Axiom 3, there exists an ant, call it A₁. Then by Axiom 1, A₁ must have two paths call them P₁ and P₂. Hence, there are at least two paths.
           We form a model that shows it is possible to have exactly two paths, which demonstrates that the minimum number of paths is two. By Axiom 2, P₁ must have an ant other than A₁, call it A₂. We form a model where A₁ and A₂ both are assigned to P₁ and P₂, then we have exactly two paths.
           We show the model satisfies all three axioms. Axiom 1 is satisfied, since A₁ and A₂ each have both P₁ and P₂.  Axiom 2 is satisfied since P₁ and P₂ each have both A₁ and A₂.  Axiom 3 is satisfied, since we have two ants.//

4. Find two nonisomorphic models.
   In the following three nonisomorphic models, the undefined terms of the axiomatic system are defined with letters to represent ants and sets of letters to represent paths. In the first model, the order of the letters for the path is necessary in order to define two distinct paths for the pair of points. Since the number of ants in each model is different, a one-to-one correspondence cannot be formed. Hence the models are nonisomorphic. Also note that each of the three axioms is satisfied for each model.

   Ant	Path	Ant	Path	Ant	Path
   A, B	AB, BA	A, B, C	{A,B}, {A,C}, {B,C}	A, B, C, D, E	{A,B}, {B,C}, {C,D}, {D,A}, {A,E,C}, {B,E}

   In the following three diagram models, let a dot represent an ant and a segment represent a path. Also note that the three models below are isomorphic to the corresponding three models above. The correspondence can be shown by labeling each point.

        

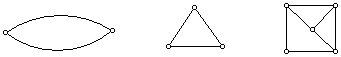
    Additional Important Comments.
           Since three of the above models are nonisomorphic, we have shown the system is not categorical.
           The above models have shown the axiomatic system is consistent.  The first three models are abstract models, which shows that the axiomatic system is relatively consistent. The above picture models are adapted from the "real-world"; therefore, they are concrete models. These concrete models  for the axiomatic system demonstrate that the axiomatic system is absolutely consistent.
           Since three of the above models are nonisomorphic, not every statement containing undefined and defined terms for this system can be proved (from the axioms) valid or invalid. Hence this axiomatic system is not complete. For example, consider the statement "There exist at least four ants." This statement cannot be proved valid or invalid by using only the axioms, since we can produce a model where the statement is valid and a model where the statement is invalid. In this example, we are able to show the system is incomplete, which is much easier to show than completeness. See the comments on Gödel's Incompleteness Theorem.

5. Show the axioms are independent.
           We need to produce a model that does not satisfy the axiom we are showing to be independent but does satisfy the other two axioms. This demonstrates that the axiom cannot be proved using the other two axioms, i.e., the axiom cannot be a theorem.
           First, we show Axiom 1 is independent. In the following model, Axiom 2 and Axiom 3 are true, but Axiom 1 is not true. Axiom 1 is not true since ant A has only one path AB. Axiom 2 is true, since path AB has two ants A and B. Axiom 3 is true, since there exists an ant A.                               

   Ant	Path
   A, B	AB

           Next, we show Axiom 2 is independent. The following model has Axiom 1 and Axiom 3 true, but Axiom 2 is not true. Axiom 1 is true, since the ant is the dot with two paths represented by the segments. Axiom 2 is not true, since each path (segment) has only one ant (dot). Axiom 3 is true, since there is one ant represented by the dot.

                          The dot is an ant and segments are paths.

           Finally, we show Axiom 3 is independent. A model where Axiom 1 and Axiom 2 are true, but Axiom 3 is not true. Consider a model with no ants and no paths. The model satisfies both Axiom 1 and Axiom 2 vacuously. But, since there are no ants, Axiom 3 is not true.
           Important reminder from logic. To understand a statement being vacuously true, we review a concept from logic. Axiom 1 is actually a conditional statement that could be stated as "If an ant exists, then it has at least two paths." With no ants and no paths, both the antecedent and consequent of the conditional are false. When a conditional has both a false antecedent and consequent, the conditional is a true statement. Note a conditional is also a true statement when the antecedent is false and the consequent is true. In either case, mathematicians say the statement is vacuously true.

6. Write the dual of this system.
   The dual of this axiomatic system is formed by interchanging ant and path in each axiom.
   Dual of Axiom 1.  Every path has at least two ants.
   Dual of Axiom 2.  Every ant has at least two paths.
   Dual of Axiom 3.  There exists at least one path.

7. How do the system and its dual compare?
   Axiom 1 and Axiom 2 are duals of each other. Axiom 3 is the dual of  Theorem 1. Hence the system and its dual are equivalent. Therefore, this axiomatic system satisfies the principle of duality.

Example 2. Consider the following axiom set.

Axiom 1.  Every ant has at least two paths.
Axiom 2.  Every path has at least two ants.
Axiom 3.  There exists exactly two ants.
Axiom 4.  Any two paths have at most one ant in common.

Show this axiom set is not consistent.
By Axiom 3, there are two ants A and B. By Axiom 1, ant A must have two paths p and q. By Axiom 2, path p must have two ants since by Axiom 3 there are only two ants these two ants must be A and B. Similarly, path q must have the two ants A and B. Hence, paths p and q both have ants A and B. But this is a contradiction since by Axiom 4 paths p and q can only have one of the two ants A or B in common. Thus, Axiom 4 is not consistent with the other three axioms; therefore, the axiom set is not consistent. //

The following exercises are written to further develop an understanding of the terms and concepts described in section 1.1.1 Introduction to Axiomatic Systems. The theorems may not be numbered in the order you need to prove them, but make sure you do not use circular reasoning. Solutions for selected problems are available in the solutions section of the Chapter One table of contents.

Exercise 1.1. Consider the following axiom set. 

Postulate 1. There are at least two buildings on campus.
Postulate 2. There is exactly one sidewalk between any two buildings.
Postulate 3. Not all the buildings have the same sidewalk between them.

1. What are the primitive terms in this axiom set?

2. Deduce the following theorems:
        Theorem 1. There are at least three buildings on campus.
        Theorem 2. There are at least two sidewalks on campus.

3. Show by the use of models that it is possible to have
       exactly two sidewalks and three buildings;
       at least two sidewalks and four buildings; and,
       exactly three sidewalks and three buildings.

4. Is the system complete? Explain.

5. Find two isomorphic models.

6. Demonstrate the independence of the axioms.

Exercise 1.2. Consider the following axiom set.  

A1.   Every hive is a collection of bees.
A2.   Any two distinct hives have one and only one bee in common.
A3.   Every bee belongs to two and only two hives.
A4.   There are exactly four hives.

1. What are the undefined terms in this axiom set?

2. Deduce the following theorems:
       T1. There are exactly six bees.
       T2. There are exactly three bees in each hive.
       T3. For each bee there is exactly one other bee not in the same hive with it.

3. Find two isomorphic models.

4. Demonstrate the independence of the axioms.

Exercise 1.3. Consider the following axiom set.

P1. Every herd is a collection of cows.
P2. There exist at least two cows.
P3. For any two cows, there exists one and only one herd containing both cows.
P4. For any herd, there exists a cow not in the herd.
P5. For any herd and any cow not in the herd, there exists one and only one other herd containing the cow and not containing any cow that is in the given herd.

1. What are the primitive terms in this axiom set?

2. Deduce the following theorems:
       T1. Every cow is contained in at least two herds.
       T2. There exist at least four distinct cows.
       T3. There exist at least six distinct herds.

3. Find two isomorphic models.

4. Demonstrate the independence of the axioms.

Mathematicians boast of their exacting achievements, but in reality they are absorbed in mental acrobatics and contribute nothing to society.
—Sorai Ogyu (1666–1728)
 

1.1.1 Axiomatic Systems1.1.3 Historical Overview

© Copyright 2005, 2006, 2007 - Timothy Peil