A Finite Geometry Exercise 1.6.
Why, I have not failed, I've just found 10,000 ways that won't work.
—Thomas Edison (1847–1931)

Exercise 1.6. Show the Fano's axioms are independent.

Axiom 1. There exists at least one line.
A model with one point and no lines does not satisfy Axiom 1, but satisfies the other axioms vacuously.

Axiom 2. Every line has exactly three points incident to it.
Points: A, B, C.  Lines: AB, AC, BC.
Axiom 2 is not satisfied, since line AB contains only two points.
Axiom 1 is satisfied, since AB is a line.
Axiom 3 is satisfied, since C is not on line AB. (Check the other cases.)
Axiom 4 is satisfied. (Check to verify.)
Axiom 5 is satisfied. (Check to verify.)

Axiom 3. Not all points are incident to the same line.
Points: A, B, C. Line: {A, B, C}.
Axiom 3 is not satisfied, since there is no point that is not on the only line {A, B, C}.
Axiom 1 is satisfied, since {A, B, C} is a line.
Axiom 2 is satisfied, since the only line {A, B, C} has the three points A, B, and C.
Axiom 4 is satisfied, since each pair of points is incident with the only line.
Axiom 5. is satisfied vacuously.

Axiom 4. There is exactly one line incident with any two distinct points.
Use the model in the illustration with one less line.
Points: A, B, C, D, E, F.  Lines: ADB, AGE, AFC, BEC, BGF, CGD.
Axiom 4 is not satisfied, since points D and F are not incident with any lines.
(Check to verify the other axioms are satisfied.)

Axiom 5. There is at least one point incident with any two distinct lines.
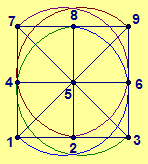Points: 1, 2, 3, 4, 5, 6, 7, 8, 9. 
Lines: 123, 456, 789, 147, 258, 369, 159, 357, 168, 348, 267, 249.

Axiom 5 is not satisfied, since lines 123 and 456 have no points incident to both lines.
(Check to verify the other axioms are satisfied.)