TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

2.5.1 Supplement Postulate  Printout
A work of morality, politics, and criticism will be more elegant, other things being equal, if it is shaped by the hand of geometry.
—Bernard le Bovier de Fontenelle (1657–1757)

 

Definitions.
      Two distinct angles are said to be supplementary angles if the sum of their measures is 180.
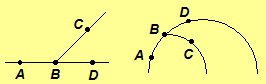
      Two angles  are a linear pair if B is between A and D. (Two left-hand figures below – Euclidean and Poincaré Half-plane.)
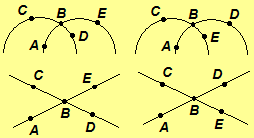
      Two angles  are vertical angles if either A-B-E and C-B-D, or A-B-D and C-B-E. (Four right-hand figures below – Poincaré Half-plane and Euclidean.)

                          
                        Linear Pair                                                                        Vertical Angles

Postulate 14. (Supplement Postulate) If two angles form a linear pair, then they are supplementary.

      The Supplement Postulate is not independent of the other axioms. Since the proof does not add insight into better understanding and is not simple, the statement is taken as an axiom instead of a theorem for most high school geometry courses. The proof that the Supplement Postulate is not independent is given below; Exercise 2.43 asks the reader to provide the reasons for each step of the proof.

Theorem 2.8 (Vertical Angle Theorem) Vertical angles are congruent.

 

      The next theorem, called the Crossbar Theorem, is needed to prove some of the coming theorems. The question the Crossbar Theorem addresses is: How do we know that a ray with one endpoint at a vertex of a triangle that contains an interior point of a triangle intersects the opposite side of the triangle? The answer seems obvious when using Euclidean geometry, but that is making an assumption. The result seems less obvious in the Poincaré Half-plane. Could the ray curl so that it intersects a side that contains the vertex? Or, is there a model where the ray curls in such a way that it never leaves the interior of the triangle? Again, since this is a survey course, we state the Crossbar Theorem here without proof. The theorem follows from the Plane Separation Postulate and Pasch's Postulate.

 

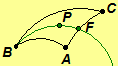
Theorem 2.9. (Crossbar Theorem) If P is an interior point of angle ABC, then ray BP and segment AC intersect in a unique point F and A-F-C.

Exercise 2.41. Find the axiom or theorem from a high school book that corresponds to the Supplement Postulate. Is it an axiom or theorem in the high school book? If it is a theorem, how was it proven?

Exercise 2.42. Prove or disprove. If two angles are supplementary, then they form a linear pair.

Exercise 2.43. Justify each numbered step and fill in any gaps in the following proof that the Supplement Postulate is not independent of the other axioms.
      We need to show that given a linear pair of angles that they are supplementary. Assume  and  form a linear pair of angles. We must show that . We do this by showing that  and  both lead to contradictions.
Case 1. Suppose .
1.  There is a unique ray BE with E and C on the same side of line AB and with .
2.  .
3.  Then .
4.  Thus .
5.  Also, .
6.  Then .
7.  Thus , which is not possible.
Case 2. Suppose .
8. 
9.  There is a unique ray BF with F and C on the same side of line AB and with .
10.  .
11.  .
12.  Thus .
13.  Hence .
14.  Also, .
15.  Then .
16.  Thus , which is not possible.
Thus, by Cases 1 and 2, we must have .

Exercise 2.44. Prove the Vertical Angle Theorem.

Exercise 2.45. Prove that two angles supplement to the same angle are congruent.

Exercise 2.46. (a)  Prove that if two congruent adjacent angles form a linear pair, then they are right angles.
                         (b) Prove that the four angles formed by two perpendicular lines are right angles.

Exercise 2.47. Prove that a segment has a unique perpendicular bisector.