Prove Theorem 2.2
"Contrariwise," continued Tweedledee, "if it was so, it might be; and if it were so, it would be; but as it isn't, it ain't. That's logic."
—
Solution
Exercise 2.12.
Prove Theorem 2.2
"Contrariwise," continued Tweedledee, "if it
was so, it might be; and if it were so, it would be; but as it isn't, it ain't.
That's logic."
—![]() Charles Lutwidge Dodgson (Lewis Carroll) (1832–1898)
Charles Lutwidge Dodgson (Lewis Carroll) (1832–1898)
Important Note. You must begin the proof by assuming two distinct lines, even though we have not shown the existence of any lines. But this is not a problem, since the statement is valid if no lines or only one line exist. The statement of the theorem is equivalent to "If two distinct lines exist, then they intersect in at most one point." Remember from logic that a conditional is always true when the antecedent is false.
Theorem 2.2. Two distinct lines intersect in at
most one point.
Proof. Let l1 and l2
be two distinct lines. Suppose l1 and l2
intersect in two distinct points P and Q. Then l1
contains P and Q and l2
contains P and Q. By Postulate 1, exactly one line contains P
and Q; therefore, l1 and l2
are the same line. But, this contradicts that l1 and l2
are distinct lines. Therefore, two lines intersect in at most one point. //
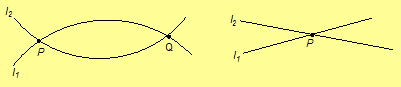
|
© Copyright 2005, 2006 - Timothy Peil |