Solution to Exercise 2.67
Euclidean Proposition 2.8.
Definition of a Commonly Used Term in Math
Similarly – At least one line of the proof of this case is the same as before.

 

Prove Euclidean Proposition 2.8. The perpendicular bisectors of the sides of a triangle intersect at a point.

 NOTE: This proof assumes that Euclidean Proposition 2.6 has already been proven.

Proof.  Given . Assume l, k, and m are the perpendicular bisectors of segments AB, BC, and AC at the points L, K, and M, respectively.

       We claim l intersects k. Suppose l does not intersect k, then l is parallel to k. Since l is perpendicular to line AB and k is perpendicular to BC, by Euclidean Proposition 2.6, line AB is parallel to line BC. But this is a contradiction since B is a point of intersection of the lines AB and BC and A, B, and C are noncollinear points. Hence l intersects k. Let P be the point of intersection of lines l and k. Similarly, we can show that l intersects m and k intersects m.

       One of the following is true: P = L, P = K, or P is neither L nor K.

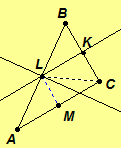       Case 1. Assume P = L. Since l bisects segment AB at L,  Since  is the perpendicular bisector of segment BC at K,  and  By the reflexive property,  Hence, by the SAS Postulate,  Hence,  Therefore,

       Since m bisects segment AC at M,   and A-M-C. By the reflexive property,  Thus, by the SSS Theorem,  Therefore,  Since  and  are a linear pair of congruent angles, line AC is perpendicular to line ML. Since there is a unique perpendicular line to line AC at M,  Hence, lines l, k, and m all intersect at P = L.

       Case 2. Assume P = K. The proof is similar to Case 1.

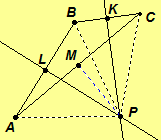       Case 3. Assume P is neither L nor K. If P = M, then we are done. Hence, assume P and M are distinct points. Since  is the perpendicular bisector of segment AB at L,  and  By the reflexive property,  Thus, by SAS Postulate,  Hence,  A similar argument shows that  Thus  By the SSS Theorem,  Hence,  Since  and  are a linear pair of congruent angles, line AC is perpendicular to line MP. Since there is a unique perpendicular line to line AC at M,  Hence, lines l, k, and m all intersect at P.//