TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

            3.2.2 An Analytic Model of the Euclidean Plane  Printout
 The intelligence is proved not by ease of learning, but by understanding what we learn.
 —Joseph Whitney

 

      To be able to define transformations in a “nice” matrix form, mathematicians modify our model of the Euclidean plane that we used in Chapter 2. The modification in the model is motivated from the standard equation for a line in the Euclidean plane, ax +by + c = 0 where a and b are not both zero. Rewrite this equation as the product of matrices to obtain the matrix equation  where a and b are not both zero. Since the coefficients a, b, and c define the line, the matrix [a, b, c] represents the line and the matrix [x, y, 1]^T (the superscript T indicates the transpose of the matrix) represents the points that satisfy the equation. Hence, for this model a line is defined by an ordered triplet or row matrix [a, b, c] and a point is defined by an ordered triplet or column matrix, the transpose of [x, y, 1]. For easier writing of points, denote a point by  (x, y, 1 ) = [x, y, 1]^T.

      The only problem with this formulation is lines do not have a unique form. Note that the standard equations 2x + 3y + 5 = 0 and 6x + 9y + 15 = 0 represent the same line. In fact, all equations of the form 2kx + 3ky + 5k = 0, where k is a nonzero real number, represent the same line as 2x + 3y + 5 = 0. Define an equivalence relation

[a₁, a₂, a₃]  [b₁, b₂, b₃], if b_i = ka_i, i = 1, 2, 3 where  

We modify the above definition of a line as the equivalence class of ordered triples (row matrix) [a₁, a₂, a₃] where a₁ and a₂ are not both zero.

      Since the form for the line and point are motivated from a homogeneous matrix equation, we call the row matrix [a₁, a₂, a₃], the homogeneous coordinates of a line, and the column matrix (x₁, x₂, 1), the homogeneous coordinates of a point.
      We summarize the definitions of the undefined terms point, line, and incident for this model of the Euclidean plane.

point	A column matrix denoted by (x1, x2, 1).
line	An equivalence class of row matrices [a1, a2, a3] where a1 and a2 cannot both be zero.
incident	A point X(x1, x2, 1) is incident with a line l[l1, l2, l3] iff lX = 0.

 

      What happens with this model when three distinct points are collinear? Let (x₁, x₂, 1), (y₁, y₂, 1), and (z₁, z₂, 1) be three distinct collinear points. Since the points are collinear, there is a line [a₁, a₂, a₃] that all three points satisfy, i.e.,

, ,  

or

a₁x₁ + a₂x₂ + a₃ = 0
a₁y₁ + a₂y₂ + a₃ = 0

a₁z₁ + a₂z₂ + a₃ = 0

or

 

From linear algebra, a homogeneous equation has a nontrivial solution [a₁, a₂, a₃] if and only if

 

We have proven one direction of the following theorem. See Exercise 3.17 to complete the proof.//

 

Proposition 3.1. Three distinct points (x₁, x₂, 1), (y₁, y₂, 1), and (z₁, z₂, 1) are collinear if and only if the determinant

 

Note that Proposition 3.1 implies that a line through two distinct points (a₁, a₂, 1), and (b₁, b₂, 1) may be written as

 

A similar theorem may be stated for three distinct lines being concurrent. A set of lines is concurrent if the lines have a common point of intersection.

 

Proposition 3.2. Three distinct lines l, m, and n are all concurrent or all parallel if and only if the determinant

 

Note that Proposition 3.2 implies that a point on two distinct lines [p₁, p₂, p₃], and [q₁, q₂, q₃] may be found from the equation

 where l represents an arbitrary unknown line.

 

Example. Find the point of intersection of lines [1, 1, 1] and [2, 1, –1].

 iff  2l₁ – 3l₂ + l₃ = 0  iff  .

Hence the point of intersection is (2, –3, 1). Note: The third position of the point in this model must be a one. If it is not a one, then form the equivalent column matrix that has a one in the third position.

 

       The formula for the distance between two points X(x₁, x₂, 1) and Y(y₁, y₂, 1) is the usual Euclidean distance formula .

       Next, consider the angle between two lines p[p₁, p₂, p₃], and q[q₁, q₂, q₃]. 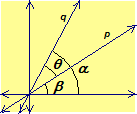Let where α and β are are the measures of the angles formed by the x-axis with the lines p and q, respectively. Remember the slope of a line through the origin and the tangent of the angle formed by the line with the x-axis are related,  and . Use a difference of two angles identity from trigonometry to obtain

.

This trigonometry result motivates the definition of the measure of the angle between two lines p and q,

 where , if
, if .

Unlike in the motivation, the definition is for any two lines.

 

Exercise 3.6. Find two lines l[l₁ ,l₂, l₃] through the point (2, –3, 1).

 

Exercise 3.7. Given the line [4, –2, 3]. (a)  Write two other sets of homogeneous coordinates for the line. (b)  Write an equation of the line.  (c)  Find two distinct points (x₁, x₂, 1) on the line.

 

Exercise 3.8. Find the line l[l₁, l₂, l₃] for each problem. (a)  x₁-axis.  (b)  x₂-axis.  (c)  The line where all points have the same first and second coordinates.

 

Exercise 3.9. (a)  What are the coordinates of the origin?  (b)  Find the general form of a line l[l₁, l₂, l₃] through the origin.

 

Exercise 3.10. Find the two lines l[l₁, l₂, l₃] that represent the two coordinate axes.

 

Exercise 3.11. Find the line l[l₁, l₂, l₃] that contains the points (3, 5, 1) and (–7, 3, 1).

 

Exercise 3.12. Find the point of intersection of the lines [–2, 4, –3] and [3, –5, 2].

 

Exercise 3.13. Use the propositions to justify your answer for the following. (a) Are the points (8, 2, 1), (7, 5, 1), and (5, 11, 1) collinear?   (b)  Are the lines [4, 2, 3], [–3, 1, 0], and [2, –7, 3] concurrent? 

 

Exercise 3.14. Use the definition to find the measure of the angle between each pair of lines. (a)  [–2, 4, –3] and [3, –5, 2].  (b)  The coordinate axes.

 

Exercise 3.15. (a)  What is the relationship between the coordinates of two distinct parallel lines? Justify the expressions.  (b)  Based on the definition of the measure of an angle between two lines, what is the measure of the angle between two parallel lines?

 

Exercise 3.16. Prove the relation used in defining lines is an equivalence relation.

 

Exercise 3.17. The steps in the converse of the proof of Proposition 3.1 are reversible, but require that the nontrivial solution, [a₁, a₂, a₃], of the matrix equation cannot have both a₁ and a₂ be zero. Prove that this is true, which completes the proof of the proposition.

 

Exercise 3.18. Prove Proposition 3.2.