6Logic

Valid Arguments and Constructing Proofs
Reductio ad absurdem...is a far finer gambit then any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.
—Sir Godfrey Harold Hardy (1877–1947)

Theorems (proved statements) are deduced from undefined terms, defined terms, assumptions, and previously proved theorems using tautologies and valid arguments.

Reminder from earlier. A tautology is a proposition that is always true.

A list of some basic tautologies to be used:

(1) Excluded Middle
(2) Contraposition
(3) Contradiction (reductio ad absurden)
(4) Associativity and
(5) Distributivity and
(6)
(7)
(8) DeMorgan's Laws and
(9) Transitivity (Hypothetical Syllogism)
(10) Modus Ponens
(11) Modus Tollens
(12) Disjunctive Syllogism
(13) Simplification and
(14) Conjunction
(15) Addition
(16) Conditional Conclusion

If p and q are equivalent, then will always be a tautology. Some equivalent forms that are not in the above list of tautologies:

(1) p and ~(~p)
(2) and
(3) and
(4) and
(5) and
(6) and and

Definition. An argument consists of premises and a conclusion. An argument is said to be valid iff whenever the premises are all true, the conclusion is true. The definition of valid argument stated symbolically: an argument is valid iff is a tautology.

Examples.
(a) A valid argument by modus ponens: If a quadrilateral is a square, then it is a rectangle. Quadrilateral ABCD is a square. Therefore, quadrilateral ABCD is a rectangle.

Symbolic form of the argument

(b) A valid argument by transitivity: If a triangle is isosceles, then two sides of the triangle are congruent. If two sides of a triangle are congruent, then two angles of the triangle are congruent. Therefore, if a triangle is isosceles, then two angles of the triangle are congruent.

Symbolic form of the argument

(c) An invalid argument: The angle ABC or the angle DEF is obtuse. The angle ABC is obtuse. Therefore, the angle DEF is obtuse.

Symbolic form of the invalid argument

Definition. A proof of a theorem is a sequence of valid arguments which uses the theorem's premises and the axiomatic system's axioms to deduce a valid conclusion.

Example. Prove .
We use a two-column proof to emphasize the reasons for each valid argument.
Proof.

1.		premise
2.		premise
3.	~r	premise
4.		steps 2 and 3 disjunctive syllogism
5.	~q	step 4 simplification
6.		steps 1 and 5 modus tollens

The above example illustrates the use of a direct proof. The following charts illustrate the general forms of proofs that use the contraposition tautology or the contradiction tautology.

Contraposition Proof of
     Suppose ~q
                   (use direct proof)
     Therefore, ~p.
     Thus,
     Therefore,

Proof of p by Contradiction
     Suppose ~p
                   (use direct proof)
     Therefore, q.

     Therefore, ~q.
     Thus, , a contradiction.
     Hence, p.

These are called indirect proofs. Contraposition and contradiction are different tautology/argument/proof forms, but many mathematicians write some proofs in the form of a contradiction when they are actually completing a proof by contraposition.

To prove a statement to be false, one only needs to provide a counterexample.

Example. We prove the statement "A rectangle is a square." is false with a counterexample. Consider the rectangle in the Euclidean plane with vertices at (0, 0), (0, 2), (2, 1), and (0, 1). The sides are of lengths 1 and 2. Hence it is not a square.

We finish this logic review with a two-column proof after which we break the proof apart into its component logical arguments.
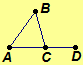
Diagram for proof that a triangle has at most one right angle.
Example. Given triangle ABC with exterior angle BCD.
Prove angle BAC and angle ACB cannot both be right angles.

	Statements	Reasons
1.	Suppose angle BAC and angle ACB are both right angles.	Assume the denial of the conclusion.
2.	Angle BCD is an exterior angle of triangle ABC.	premise
3.	The measure of angle BCD is greater than the measure of angle BAC.	An exterior angle is greater in measure than its remote interior angles.
4.	Angle ACB and angle BCD are a linear pair.	Definition of an exterior angle.
5.	Angle BCD is a right angle.	If one angle of a linear pair of angles is a right angle, then the other angle is also a right angle.
6.	The measures of angle BAC and angle BCD are equal.	All right angles have the same measure.
7.	Therefore, angle BAC and angle ACB are not both right angles.	Steps 5 and 6. A contradiction.

We symbolize the propositions.
a : Angle BAC is a right angle.
b : Angle ACB is a right angle.
c : Angle BCD is a right angle.
d : Angle BCD is an exterior angle of triangle ABC.
e : The measure of angle BCD is equal to the measure of angle BAC.
f : Angle ACB and angle BCD are a linear pair.

Consider Steps 2 and 3, we have by modus ponens that .
Consider Steps 2 and 4, we have three arguments to reach the conclusion in Step 4:

(i) an equivalency from the definition of exterior angles;
(ii) a simplification ; and
(iii) modus ponens .
Consider Steps 1, 4, and 5, we have two arguments to reach the conclusion in Step 5:
(i) a simplification ; and
(ii) modus ponens .
Consider Steps 5 and 6, we have by modus ponens that .
Finally, consider Steps 3, 6, and 7, we have by contradiction that .