TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

            Exercise 2.1. All triangles are isosceles triangles.  Printout
The truth of a theory is in your mind, not in your eyes.
—Albert Einstein (1879–1955)

Statement.  All triangles are isosceles triangles.

(a) Identify the error/s in the proof. Is the error a logic error? A bad assumption? Explain.
(b) Identify and write a definition for each term used in the statement of the theorem and proof.
(c) Identify and state any assumptions made in the proof.
(d) Identify and state any theorems used in the proof.

(Hint. If you are unable to find the errors from reading the proof, use dynamic geometry software - such as Geometer's Sketchpad or GeoGebra - to construct the figure based on the steps in the proof.)

Proof.  Given any  Let ray r be the bisector of  Let M be the midpoint of segment AB. Let l be the line perpendicular to segment AB at M.  Let D be the point of intersection of ray r and line l.

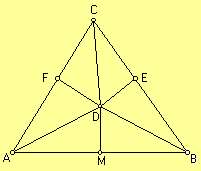
Case 1.Assume D = M. We have  and  Then , since line l is perpendicular to segment AB at M. Since M is the midpoint of segment AB,  Also,  Hence, by SAS,  Thus,  and  is an isosceles triangle.

Case 2. Assume D is distinct from M. Then , since line l is perpendicular to segment AB at M. Since M is the midpoint of segment AB,  Also,  Hence, by SAS,  Thus  Let E be the foot of the perpendicular line from D to line BC. Let F be the foot of the perpendicular line from D to line AC. Then  and  are right angles. Thus  Since ray r bisects ,  Also,  Hence, by AAS,  Thus  and  Since , , and  and  are right angles, by HL,  Hence,  Since  and , we have that

AC = AF + FC = BE + EC = BC.

Hence,  and  is an isosceles triangle.
      Therefore, since the triangle was arbitrarily chosen, all triangles are isosceles.//