TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

        2.3 Distance and Ruler Axioms  Printout
Whereas at the outset geometry is reported to have concerned herself with measurement of muddy land, she now handles celestial as well as terrestrial problems: she has extended her domain to the furthest bounds of space.
—W. B. Frankland, The Story of Euclid (1901)

 

      For most common day-to-day measurements of length, we use rulers, meter sticks, or tape measures. The distance and ruler postulates formalize our basic assumptions of these items into a general geometric axiomatic system. The SMSG Ruler Postulate defines a correspondence between the points on a line (markings on a meter stick) and the real numbers (units of measurement) in such a manner that the absolute value of the difference between the real numbers is equal to the distance (measurement of the length of an object by a meter stick matches our usual Euclidean distance). The Ruler Placement Postulate basically says that it does not matter how we place a meter stick to measure the distance between two points; that is, the origin (end of the meter stick) does not need to be at one of the two given points.

Postulate 2. (Distance Postulate) To every pair of distinct points there corresponds a unique positive number. This number is called the distance between the two points.

 

Postulate 3. (Ruler Postulate) The points of a line can be placed in a correspondence with the real numbers such that:

i.        To every point of the line there corresponds exactly one real number.

ii.      To every real number there corresponds exactly one point of the line.

iii.    The distance between two distinct points is the absolute value of the difference of the corresponding real numbers.

 

Postulate 4. (Ruler Placement Postulate) Given two points P and Q of a line, the coordinate system can be chosen in such a way that the coordinate of P is zero and the coordinate of Q is positive.

      By Proposition 2.1 and the accompanying exercises, the Euclidean plane, Taxicab plane, Max-distance plane, Missing Strip plane, Poincaré Half-plane, Modified Riemann Sphere, and discrete planes all satisfy the Distance Postulate. Tools for working with rulers in Geometer's Sketchpad are available in the Appendix B Prepared Geometer's Sketchpad and GeoGebra Sketches.

Definition. A ruler or coordinate system is a function mapping the points of a line into the real numbers, that satisfies SMSG Postulate 3.

      Note the first and second conditions of the Ruler Postulate imply that f is a one-to-one and onto function. As a reminder, we write the definitions for one-to-one and onto functions.

Definition. A function f from A to B is onto B if for any b in B there is at least one a in A such that f(a) = b.

Definition. A function f from A to B is one-to-one if for any x and y in A with  then  (Note the contrapositive of this definition is often used in writing proofs.)

Proposition 2.4. The Euclidean Plane satisfies the Ruler Postulate.

      Before we begin the proof, we do some scratch work to find the correct form for the rulers for the lines. We need a relationship between the distance and a ruler, so we begin with the distance function. First, consider a vertical line l_a, which has all the first coordinates the same.

 

This motivates the definition for the standard ruler of a vertical line l_a to be f(a, y) = y. Next, consider a nonvertical line l_m,b.

 

which motivates the definition for the standard ruler of a nonvertical line l_m,b to be .
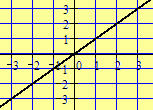       For an example, consider the simplest nonvertical line, y = x. The points (0, 0), (1, 1), (2, 2), and (3, 3) are on the line. What is the distance from (0, 0) to (1, 1)?  From (1, 1) to (2, 2)? From (1, 1) to (3, 3)?  Note the standard ruler for this line is . The coordinates for the four points determined by the standard ruler are 0, , respectively. By subtracting the appropriate coordinates of the ruler, do you obtain the distance between the points?
       In the "real-world" sense, the standard ruler (coordinate system) is the placement of a meter stick such that the zero end is at the y-axis along any line through that point on the y-axis.

Proof.  Let l be a line in the Euclidean Plane. Then l  is either a vertical line or a nonvertical line.

Case 1.  Assume l = l_a  a vertical line. Define  by f(a, y) = y. We need to show the three conditions. First, show f  is one-to-one. Let (x₁, y₁) and (x₂, y₂) be points on l_a. We have x₁ = x₂ = a.  Suppose f(x₁, y₁) = f(x₂, y₂). Then y₁ = y₂ by the definition of f.  Thus (x₁, y₁) = (a, y₁) = (a, y₂) = (x₂, y₂). Hence f  is one-to-one. We next show f is onto. Let r be any real number. Consider the point (a, r) on line l_a. Note f(a, r) = r. Hence f  maps the line onto the real numbers. Finally, we show the distance condition. Let P(x₁, y₁)  and Q(x₂, y₂) be points on line l_a. We have x₁ = x₂ = a. Thus

 

Case 2. Assume l = l_m,b is a nonvertical line. Define  by . We first show f is one-to-one. Let (x₁, y₁) and (x₂, y₂) be points on l_m,b.  Suppose f(x₁, y₁) = f(x₂, y₂). Then . Hence, x₁ = x₂. We then have y₁ = mx₁ + b = mx₂ + b = y₂. Thus (x₁, y₁) = (x₂, y₂). Hence f  is one-to-one. We next show f is onto. Let r be any real number. Consider the point . Note

.

Hence f is onto. Finally, we show the distance condition. Let P(x₁, y₁)  and Q(x₂, y₂) be points on line l_m,b.

 

Therefore, by Cases 1 and 2, an arbitrary line in the Euclidean plane has a ruler (coordinate system).//

      As was discussed in Chapter 1, axioms need not be independent, which is the case with the Ruler Placement Postulate.

Theorem 2.5. The Ruler Placement Postulate is not independent of the other axioms.

Outline of the proof. We need to show that given two distinct points P and Q on a line l, there is a ruler that satisfies the conditions that the coordinate of point P is zero, and the coordinate of point Q is positive.
      Assume  is a ruler. (Why do we know a line and a ruler exist?)
      Let P and Q be two distinct points on l.
      Set .
      Define  by g(A) = k[f(A) – f(P)] for all points A on l.  (Why is g defined this way?)
      Show g satisfies the conditions of the Ruler Postulate, i.e. show g is one-to-one, show g is onto, and show g satisfies the distance condition.
      Show g(P) = 0 and g(Q) > 0.//

 

Definitions.

      A point B is between points A and C, denoted A-B-C, if {A, B, C} is a collinear set of three distinct points and AB + BC = AC. (Here, AB represents the distance from A to B, i.e. d(A, B) = AB.)
      A line segment is the union of two distinct points and all points between those two points, denoted either as segment AB or . The points A and B are called the endpoints of segment AB.
      Two segments are congruent if they have the same measure, denoted .
      A point M  is the midpoint of segment AB if AM = MB and {A, M, B} is collinear.
      A bisector of a segment is a line that contains the midpoint of the segment.
      A ray AB is the union of the segment AB and the set of all points C such that B is between A and C, denoted either as ray AB or . The point A is called the endpoint of the ray AB. (Note ray AB and ray BA are different rays.)

      A triangle is the union of three segments determined by three noncollinear points, i,e., triangle ABC is the union of segment AB, segment AC, and segment BC. Each of the three noncollinear points that determine a triangle is called a vertex of the triangle.

 

Exercise 2.17. Find the axioms from a high school geometry book that correspond to SMSG Postulates 2, 3, and 4.

Exercise 2.18. How do the SMSG Postulates 3 and 4 relate to "real-world" applications?

Exercise 2.19. For each model (Euclidean, Taxicab, Max-Distance, Missing Strip, and Poincaré Half-plane) find a ruler where f(P) = 0 and f(Q) > 0 for (a)  P(3, 4)  and Q(3, 7); and  (b) P(–1, 3) and Q(1, 2).

Exercise 2.20. Complete the proof that the Ruler Placement Postulate is not independent, Theorem 2.5.

Exercise 2.21. Show the stated model satisfies SMSG Postulate 3, the Ruler Postulate, for  (a)  Taxicab Plane;   (b)  Max-Distance Plane;  (c)  Missing Strip Plane; and  (d)  Poincaré Half-plane.

Exercise 2.22. Does the Modified Riemann Sphere satisfy SMSG Postulate 3, the Ruler Postulate? Explain.

Exercise 2.23. Explain why collinear is necessary in the definition of betweenness. (Hint. Look for an example in either the Taxicab or Max-distance plane where the distance condition is satisfied, but the point would not be on the line.)

Exercise 2.24. Prove a segment has a unique midpoint.

Exercise 2.25. Find the midpoint of the segment AB for each model (Euclidean, Taxicab, Max-distance, Missing Strip, and Poincaré Half-Plane) where  (a) A(1, 1) and B(1, 5); and  (b)  A(–1, 1) and B(3, 2). (Show the work using the standard ruler for each model.)

Exercise 2.26. Find the ray AB for each model (Cartesian, Missing Strip, and Poincaré Half-plane) where  (a) A(–3, 1) and B(–3, 7); and  (b)  A(–1, 5) and B(3, 1).

Exercise 2.27. An equivalence relation, ~, is a relation on a set that satisfies each of the following: (i)  a ~ a  (reflexive property)  (ii) If a ~ b, then b ~ a. (symmetric property)  (iii)  If  a ~ b and b ~ c, then a ~ c. (transitive property).
      Prove that  is an equivalence relation for the set of all segments.

 

Don't measure yourself by what you have accomplished, but by what you should have accomplished with your ability.
—John Wooden (1910–2010)