Diagrams for Exercise 2.10. Sketch and describe a circle for each model.
I am interested in mathematics only as a creative art.
—Exit book to another website.Godfrey H. Hardy (1877–1947)

The equation and at least one general diagram is given for each circle with center (a, b) and radius r. Try to derive the equations for each circle.

Taxicab Circle

|x – a| + |y – b| = r Circle in the Taxicab plane 

Euclidean Circle

(x – a)2 + (y – b)2 = r2Circle in the Euclidean plane  

Max-distance Circle 

max{|x – a| , |y – b|} = r Circle in the Max-distance plane

Poincaré Half-plane Circle

(x – a)2 + (y – bcosh r)2 = (bsinh r)2 Circle in the Poincare Half-plane

Missing-Strip Circles
For 0 <= a – 1 < r and x < 0, (Euclidean otherwise) (Note the division, /, in each equation.)

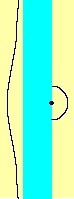
(x – a)2 + (y – b)2 = r2[1 – (2(x – a) + 1)/(x – a + 1)2] Circle in Missing-strip plane with 0 < a - 1 < ror  Circle in Missing-strip plane with 0 < a - 1 < r 

For –r < a < 0 and x >= 1, (Euclidean otherwise)

(x – a)2 + (y – b)2 = r2[1 + (2(x – a) – 1)/(x – a – 1)2]Circle in Missing-strip plane with - r < a < 0  or  Circle in Missing-strip plane with - r < a < 0


For a <= –r or a – 1 >= r,

(x – a)2 + (y – b)2 = r2    Circle in Missing-strip plane with a <= - r

Solutions for Chapter 2Back to Solutions for Chapter Two.

Ch. 2 Euclidean/NonEuclidean TOC  Table of Contents

  Timothy Peil  Mathematics Dept.  MSU Moorhead

© Copyright 2005, 2006 - Timothy Peil