Solution to Exercise 2.67
Euclidean Proposition 2.8.
Definition of a
Commonly Used Term in Math
Similarly – At least one line of the proof of this case
is the same as before.
Prove Euclidean Proposition 2.8. The perpendicular bisectors of the sides of a triangle intersect at a point.
NOTE: This proof assumes that Euclidean Proposition 2.6 has already been proven.
Proof.
Given .
Assume l, k, and m are the perpendicular bisectors of segments
AB,
BC, and
AC at the
points L, K, and M, respectively.
We claim l intersects k. Suppose l does not intersect k, then l is parallel to k. Since l is perpendicular to line AB and k is perpendicular to BC, by Euclidean Proposition 2.6, line AB is parallel to line BC. But this is a contradiction since B is a point of intersection of the lines AB and BC and A, B, and C are noncollinear points. Hence l intersects k. Let P be the point of intersection of lines l and k. Similarly, we can show that l intersects m and k intersects m.
One of the following is true: P = L, P = K, or P is neither L nor K.
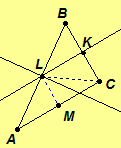 Case 1. Assume P = L. Since l bisects segment AB at L,
Case 1. Assume P = L. Since l bisects segment AB at L, Since
is the perpendicular bisector of segment
BC at K,
and
By the reflexive property,
Hence, by the SAS Postulate,
Hence,
Therefore,
Since m bisects segment
AC at M, and A-M-C. By the reflexive property,
Thus, by the SSS Theorem,
Therefore,
Since
and
are a linear pair of congruent angles, line AC is perpendicular to line ML. Since there is a unique
perpendicular line to line AC at M,
Hence, lines l, k, and m all intersect
at P = L.
Case 2. Assume P = K. The proof is similar to Case 1.
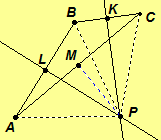 Case 3. Assume P is neither L nor K. If P = M, then we are done.
Hence, assume P and M are distinct points. Since
Case 3. Assume P is neither L nor K. If P = M, then we are done.
Hence, assume P and M are distinct points. Since is the perpendicular bisector of segment
AB at L,
and
By the reflexive property,
Thus, by SAS Postulate,
Hence,
A similar argument shows that
Thus
By the SSS Theorem,
Hence,
Since
and
are a linear pair of congruent angles, line AC is perpendicular to line MP. Since there is a unique
perpendicular line to line AC at M,
Hence, lines l, k, and m all intersect at P.//