Solution to Exercise 2.55.
Perfect
numbers like perfect men are very rare..
—![]() Rene Descartes (1596–1650)
Rene Descartes (1596–1650)
Exercise
2.55. For the Poincaré Half-plane, find all lines parallel to the given
line through the given point.
(a)
(2, 1) and
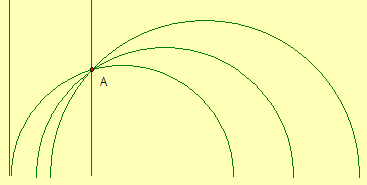
Note that for a Type II line parallel to the given line, c must be
greater than 1 and r must be less than or equal to the distance from c to 1.
Hence, the line must satisfy (2 – c)2
+12 = r2 and Hence,
Solving yields
Therefore, the line 2l and the lines
where
and
are parallel to the line
1l and pass through the point (2, 1).
(b)
(2, 1) and
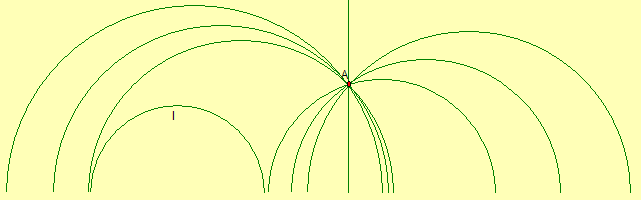
Either the same as part (a) or the
line where c < 1 must have r greater than or equal to the distance
from c to –1. Hence, the line must satisfy
and
Hence,
Solving the inequality yields
Therefore, the line 2l and the lines
where
or
and
are parallel to the line
and pass through the point (2, 1).