Statistical Research for Behavioral Sciences
Brian G. Smith, Ph.D.
Lesson - 10
You may also check your understanding of the material on the Wadsworth web site. Click on the Publisher Help Site button.
![]()
Homework - Lesson 10
Any student may may do the assignments from any area. You may run through this work an unlimited number of times. If you make errors, you will be referred to the appropriate area of the book for re-study.
.
Assessment - Lesson 10
You will have two options to take the quiz. If you fail to achieve 100% on the quiz, you will not able to advance to the next lesson. After failing on the second take, please email the instructor at ed602@mnstate.edu so remedial action can be taken.
| Homework and Quizzes are on Desire 2 Learn. Click on the Desire 2 Learn link, log in, select the Homework/Quizzes icon and choose the appropriate homework or quiz. |
![]()
Assignments and Information
Notes
Inferential Statistics
-
Used when an entire population can not be measured
-
Used to draw inferences from a sample that can be applied or generalized to a population
-
Are just an estimate of what the parameters of a population could be
-
Point estimation, estimating the value of a parameter as a single point
-
Unbiased estimator, a statistic with a mean value over an infinite number of random samples equal to the parameter it estimates, for example, mean.
-
Biased estimators consistently over or under estimate the parameter it estimates, like sample variance always underestimates population variance
-
Consistent estimator, a statistic for which the probability that the statistic has a value closer to the parameter increases as sample size increases, for example the sample mean.
-
Sampling Methods – a number of sampling methods have been set up to ensure that a sample is representative of the population from which it is selected.
-
Simple random sampling
-
Each member of the population has an equal chance of being selected for the sample
-
The selection of one member is independent of the selection of any other member
-
Can use physical mixing process, names in a hat, coin flips, lottery system or mathematical mixing like random number tables
-
You can randomly select who will be in your sample and randomly assign subjects to treatment groups
-
-
Stratified random sampling
-
Members of a population are organized into subgroups, or strata
-
Members of the population are randomly selected from the strata in either equal proportions, or proportions that match the general population
-
Sampling distributions
-
Frequency distribution of the statistics from multiple random samples
-
You need to use the same statistic throughout, if you start using means, don’t switch to medians
-
All samples need to be the same size, all samples of 25 scores rather than some samples with 20 scores, some 25 and a few 30 scores
-
Use random samples
-
-
Allows for a conclusion
-
Estimated mean
-
Estimated error
-
Central limit theorem - As a sample size increases, the sampling distribution of the mean will approach a normal distribution.
-
Sampling Error – the amount by which a particular sample mean differs from the population mean
-
Standard Error – the standard deviation of the sampling distribution of the mean
Confidence Intervals
-
A range of score values expected to contain the population mean
-
Confidence limits are the lowest and highest scores of the confidence interval
-
The most common confidence intervals are for 68%, 95%, and 99%, with 95% and 99% being used most often in research
-
Confidence intervals are built using z scores and the z score table on pages 487-490 in the text
The larger the sample size the smaller your confidence interval will be. So now we will take this information and look at our BASC study. We know from previous chapters that for our sample of 25 students we have a mean of 51.4 points and an estimated population standard deviation of 11.12 points. What would be our standard error?
Which we round to 2.22 for significant digits. Notice that we are dividing our standard deviation by the number of subjects in our sample. That means that if we use a larger sample, like 100 and get the same standard deviation, we get a lower number for our standard error.
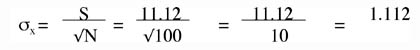 |
So now we can find a 95% confidence interval using our standard error. We know from previous chapters that 95% of our scores will fall between z scores of –1.96 and +1.96. We can find the lower confidence limit by using the formula from your text on page 141.
We round this to 47.05. Then we find the upper limit the same way.
We round this to 55.75, giving us a 95% confidence interval of 47.05 to 55.75 points on the BASC.
| SPSS Tips: |
 |
Vocabulary
Statistical inference – Estimating population values from statistics obtained from a sample. Because we are giving the BASC survey to only a small sample of students we will use statistical inference to see if the BASC survey is culturally biased against Hispanic teens.
Point estimation – Estimating the value of a parameter as a single point from the value of a statistic. We will be using point estimation to say that the mean we get for our sample is the same as the mean that we would get if we surveyed the entire population.
Unbiased estimator – A statistic with a mean value over an infinite number of random samples equal to the parameter it estimates. The mean of our BASC scores is an unbiased estimator, because if we took a dozen samples of 25 students, the mean for the dozen samples would be very close to the mean of our original sample. Sample variance is a biased estimator, because it consistently underestimates the variance of the population.
Simple random sampling – Selecting members from a population such that each member of the population has an equal chance of being selected for the sample and the selection of one member is independent of the selection of any other member of the population, also known as random sampling. If we put the names of all the students in our school in a hat and drew 25 names, that would be a simple random sample of our students.
Stratified random sampling – A sampling method in which members of a population are categorized into homogeneous subgroupings called strata. Members of the population are randomly sampled from the strata in the proportion to which the strata occur in the population. For our BASC study, we are placing our students into strata by cultural background before drawing names from the hat.
Systematic sampling – A procedure in which every nth person in line or on a list is chosen for the sample. If we don’t have a hat or a random number table handy, we can list all the names on a page and take every 10th person to fill our sample.
Cluster sampling – Randomly choosing intact groups like families, classes, offices, rather than individuals. For simplicity purposes, it would be possible to have intact groups take the survey. If you could make sure that all the students in 7th hour English are not Hispanic, and all the students in 3rd hour English as a Learned Language class are, then you could give the survey to those two intact groups.
Sampling distribution – A theoretical probability distribution of values of a statistic resulting from selecting all possible samples of size N from a population. This is like a frequency distribution, but you graph statistics, like mean or mode, rather than raw scores.
Sampling distributions of the mean – The distribution of mean values when all possible samples of size N are selected from a population.
Central limit theorem – A mathematical theorem stating that, as a sample size increases, the sampling distribution of the mean approaches a normal distribution.
Sampling error – The amount by which a sample mean differs from a population mean.
Standard error of the mean (Joe, please insert the symbol mu sub x bar from page 135 here) – the standard deviation of the sampling distribution of the mean found by dividing s by the square root of the size of the sample. The standard error for our BASC scores happens to be 2.22 points.
Confidence interval – A range of score values expected to contain the value of m with a certain level of confidence. The 95% confidence interval for our BASC scores is from 47.05 to 55.75 points. We are 95% certain that the true population mean is within this range of scores.
Confidence limits – The lower and upper scores defining the confidence interval. The lower confidence limit for our 95% confidence interval is 47.05. The upper limit is 55.75.
