1.       Imagine a society that produces military goods and consumer goods, which we’ll call “guns” and “butter.”

a.       Draw a production possibilities frontier for guns and butter. Using the concept of opportunity cost, explain why it is most likely has a bowed-out shape.

b.      Show a point that is impossible for the economy to achieve. Show a point that is feasible but inefficient.

c.       Imagine that the society has two political parties, called the Hawks (who want a strong military) and the Doves (who want a smaller military). Show a point on your production possibilities frontier that the Hawks might choose and a point that the Doves might choose.

d.      Imagine that an aggressive neighboring country reduces the size of its military. As a result, both the Hawks and the Doves reduce their desired production of guns by the same amount. Which party would get the bigger “peace dividend,” measured by an increase in butter production? Explain.

a.   The Figure below shows a production possibilities frontier between guns and butter. It is bowed out because the opportunity cost of butter depends on how much butter and how many guns the economy is producing. When the economy is producing a lot of butter, workers and machines best suited to making guns are being used to make butter, so each unit of guns given up yields a small increase in the production of butter. Thus, the frontier is steep and the opportunity cost of producing butter is high. When the economy is producing a lot of guns, workers and machines best suited to making butter are being used to make guns, so each unit of guns given up yields a large increase in the production of butter. Thus, the frontier is very flat and the opportunity cost of producing butter is low.

Figure

      b.   Point A is impossible for the economy to achieve; it is outside the production possibilities frontier. Point B is feasible but inefficient because it is inside the production possibilities frontier.

      c.    The Hawks might choose a point like H, with many guns and not much butter. The Doves might choose a point like D, with a lot of butter and few guns.

      d.   If both Hawks and Doves reduced their desired quantity of guns by the same amount, the Hawks would get a bigger peace dividend because the production possibilities frontier is much flatter at point H than at point D. As a result, the reduction of a given number of guns, starting at point H, leads to a much larger increase in the quantity of butter produced than when starting at point D.

2.       An economy consists of three workers: Larry, Moe, and Curly. Each works ten hours a day and can produce two services: mowing lawns and washing cars. In an hour, Larry can either mow one lawn or wash one car; Moe can either mow one lawn or wash two cars; and Curly can either mow two lawns or wash one car.

a.       Calculate how much of each service is produced under the following circumstances, which we label A, B, C, and D:

·   All three spend all their time mowing lawns. (A)

·   All three spend their time washing cars. (B)

·   All three spend half their time on each activity. (C)

·   Larry spends half of his time on each activity, while Moe only washes cars and Curly only mows lawns. (D)

b.      Graph the production possibilities frontier for this economy. Using your answers to part (a), identify points A, B, C, and D on your graph.

c.       Explain why the production possibilities frontier has the shape it does.

d.      Are any of the allocations calculated in part (a) inefficient? Explain.

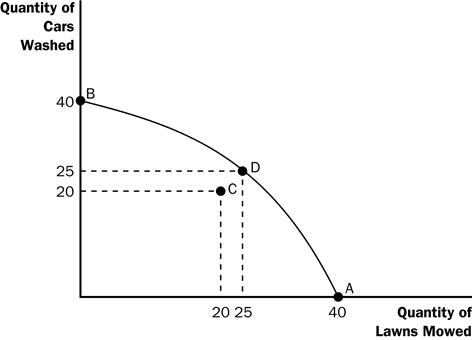
a.   A: 40 lawns mowed; 0 washed cars

            B: 0 lawns mowed, 40 washed cars

            C: 20 lawns mowed; 20 washed cars

            D: 25 lawns mowed; 25 washed cars

Figure

b.   The production possibilities frontier is shown in the Figure above. Points A, B, and D are on the frontier, while point C is inside the frontier.

 c.    Larry is equally productive at both tasks. Moe is more productive at washing cars, while Curly is more productive at mowing lawns.

 d.   Allocation C is inefficient. More washed cars and mowed lawns can be produced by simply reallocating the time of the three individuals.

3.        Michael and Angelo live in a small town in Italy.  They work as artists.  Michael is the more productive artist.  He can produce 10 small sculptures each day but only 5 paintings.  Angelo can produce 6 sculptures each day but only 2 paintings.

a.       What is the opportunity cost of a painting for each artist?

b.      Based on you answer in part a, who has the comparative advantage in producing paintings.

c.       If the two men decide to specialize, who should produce the sculptures and who should produce the paintings.

a.  Michael's opportunity cost is 2 sculptures for each painting he produces.  How do we know this?  If he devotes all of  his time to sculptures, he can produce 10.  If he devotes all of his time to paintings, he can produce 5.  The ratio 10:5 is the same as 2:1.  Michael is therefore twice as fast at producing sculptures as he is at producing paintings.  Angelo's opportunity cost is 3 sculptures for each painting he produces.  If he devotes all of his time to sculptures, he can produce 6.  If he devotes all of his tome to paintings, he can produce 2.  The ratio 6:2 is the same as 3:1.

b.  For this question, we need to compare Michael's and Angelo's relative strengths.  Michael produces 2 sculptures for every painting, and Angelo produces 3 sculptures for every painting.   Since Michael is only twice as good at producing sculptures, his opportunity cost of producing paintings is 2 sculptures instead of 3.  Therefore, Michael is the low-opportunity-cost producer of paintings.

c.  If they specialize, Michael should paint and Angelo should do sculptures.  You might be tempted to argue that Michael should just work alone, but if Angelo does the sculptures it frees up Michael to concentrate on the paintings.  This is what comparative advantage is all about.

4.       Should Prof. Stutes, who has highly specialized training in economics, take time out of office hours for students to type homework assignments.  Defend your answer with the concepts we have learned in this chapter.

Look back at the answer 3 c.  It is the same.  Although I may have an absolute advantage at both, I can not have a comparative advantage at both and; therefore, trade will improve the situation.

5.       Two friends, Becky and Jesse enjoy baking bread and making apple pies.  Becky takes 2 hours to bake a loaf of bread and 1 hour to make a pie.  Jesse takes 4 hours to bake a loaf and 4 hours to make a pie.

a.       What are Becky’s and Jesse’s opportunity cost of baking bread?

b.      Who has an absolute advantage at making bread?

c.       Who has a comparative advantage at making bread?

d.      If Becky and Jesse each decide to specialize in order to increase their joint production, what should Jesse produce?  What should Becky produce?

e.      (Bonus)  The price of a loaf of bread can be expressed in terms of an apple pie.  If Jesse and Becky are specializing in production and each decides to trade with each other, what range of ratios of bread and apple pie would allow both parties to benefit from trade.

a.  Becky gives up 2 pies for every loaf she makes.  Jesse gives up 1 pie for every loaf he makes.

b.  Becky

c.  Jesse

d.  Jesse should make the bread and Rachel the pies.

e.  Becky makes 2 pies per loaf and Jesse make 1 pie per loaf.  So any trade between 2:1 and 1:1 would benefit them both

6.       Are the following statements true or false?  Explain in each one.

a.       Two countries can achieve gains from trade even if one of the counties has an absolute advantage in production of all goods.

b.      Certain very talented people have a comparative advantage in everything they do.

c.       If a certain trade is good for one person, it cannot be good for another one.

d.      If a trade is good for a country, it must be good for everyone in the country.

a.   True; two countries can achieve gains from trade even if one of the countries has an absolute advantage in the production of all goods. All that is necessary is that each country have a comparative advantage in some good.

 b.   False; it is not true that some people have a comparative advantage in everything they do. In fact, no one can have a comparative advantage in everything. Comparative advantage reflects the opportunity cost of one good or activity in terms of another. If you have a comparative advantage in one thing, you must have a comparative disadvantage in the other thing.

 c.    False; it is not true that if a trade is good for one person, it cannot be good for the other one. Trades can and do benefit both sides¾especially trades based on comparative advantage. If both sides did not benefit, trades would never occur.

 d.   False; to be good for both parties, the trade price must lie between the two opportunity costs.

 e.   False; trade that makes the country better off can harm certain individuals in the country. For example, suppose a country has a comparative advantage in producing wheat and a comparative disadvantage in producing cars. Exporting wheat and importing cars will benefit the nation as a whole, as it will be able to consume more of all goods. However, the introduction of trade will likely be harmful to domestic auto workers and manufacturers.

7.       The United States exports corn and aircraft to the rest of the world and it imports oil and clothing from the rest of the world.  Do you think this pattern of trade is consistent with the principle of comparative advantage?  Why or why not?

This pattern of trade is consistent with the principle of comparative advantage. If the United States exports corn and aircraft, it must have a comparative advantage in the production of these goods. Because it imports oil and clothing, the United States must have a comparative disadvantage in the production of these items.