Chapter 3.1 and 6: Long Run Economic Growth
There is no one answer to how why the economic growth of one
nation is greater than another, but economic theory has provided many insights
which help to explain portions of the growth process. Again the saving
investment decision will play a key role as does the productivity of labor.
Chapter 3
I. The Production Function: Shows how much output the economy produces
with given amounts of labor and capital.
A. Factors of production:
What is used in the production process?
1. Capital
2. Labor
3. Other (raw materials, land energy…)
4. Productivity of factors depends on technology and management productivity
refers to the return received from inputs, if there is an increase in
productivity each unit of input (Capital, Labor or other) will produce more
output.
B. Production function: A mathematical expression relating the amount of
output produced to the quantities of capital and labor used.
Y=Af(K,L)
Where: Y= real output in a given time period
A= a measure of productivity
K= the capital stock used in the period
L= the number of workers employed ( the labor input)
f= a function relating Y to K and N
Example:
Y=A(K0.5N 0.5) Note: A
variable raised to the 0.5 power is the same as taking the square root of the
variable
Let K = 2500, n = 9000, A =2 then output would be equal to:
Y = 2(2500.059000.5) =2(50*30) =2 (1500) = 3000
What if productivity doubles to 4? Then output would increase to 6000.
What would cause this to happen?
C. Above is an example of a Cobb Douglas production function Y= A KaN1-a
good approximation for the US economy is when a is equal to 0.3
D. The shape of the production function:
Easiest way to graph the production function is by keeping the measure of
productivity and amount of one of the factors (capital or labor) constant,
allowing the other to vary.
For now assume that the amount of capital is held constant and labor is
allowed to vary.
a. The production function slopes upward from left to right
b. The slope of the production function becomes flatter form left to
right.
E. The marginal productivity of labor: How much does an additional unit of
labor increase output? It will it be equal to the slope of the line tangent to
the production function at a particular point.
a. The marginal productivity of capital will always be positive.
b. Diminishing marginal productivity of labor: (each additional unit will
result in a smaller increase in output)
F. Supply Shocks
A change in the amount of output which can be produced for a given amount
of labor and capital (also termed a productivity shock)
a. Positive supply shock causes the slope of the production function to
increase at every level of output (the production function shifts upward).
b. Negative supply shock causes the slope of the production function to
decrease at every level of output (the production function shifts
downward).
I. The Sources of Economic Growth (6.1)
A. The production function Y = A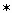 F(K,N) from Chapter
3
F(K,N) from Chapter
3
For the quantity of output to increase one of the factors of production
must increase otherwise output will stay constant and there will be no
growth in the economy.
1) The rate of growth of output can be represented by:
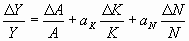
Where: ∆Y/Y = The Rate of growth of output
∆A/A = The Rate of growth of productivity
∆K/K = The Rate of Growth of Capital
∆N/N = The Rate of Growth of Labor
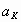 = elasticity of output with respect to capital
= elasticity of output with respect to capital
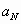 = elasticity of output with respect to labor
= elasticity of output with respect to labor
Both 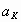 and
and 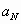 are less than
one due to diminishing marginal returns
are less than
one due to diminishing marginal returns
B. Growth Accounting: Measuring the relative importance of the different
factors of growth
need to break the growth in output into its components productivity
growth, capital input growth and labor input growth. Then what is left over
is attributable to growth in total factor productivity or ∆A/A
Procedure to find this:
1) Get data on ∆Y/Y, ∆K/K, and ∆N/N adjust for quality
changes
2) Estimate 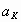 and
and 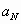 from the
data
from the
data
3) Calculate the contribution of K and N using 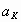 ?K/K
and
?K/K
and 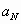 ?N/N
?N/N
4) Calculate productivity growth as the residual :
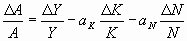
C. Application to US Economy
II. Growth Dynamics: The Solow Model
Allows capital to vary (as opposed to chapter 3) attempts to explain how
economic growth and capital accumulation are interrelated. We will use it to
examine three basic questions
1. What is the relationship between a nations long run standard of living and
fundamental factors such as its saving rate, its
population growth rate, and its rate of technical progress?
2. How does a nation’s rate of economic growth evolve over time? Will economic
growth stabilize, accelerate or stop?
3. Do economic forces exist that will ultimately allow poorer countries to catch
up with the richest countries in terms of standard
of living?
A. Setup of the Solow Model
1. Basic assumptions
a. Population and work force grow at the same rate n.
b. Closed economy and there are no government purchases of goods and
services therefore
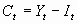
c. Rewrite the equation in per capita (per worker) terms by dividing by
the size of the labor force Nt Denote per worker values in
lower cases
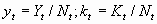
d. kt is the capital – labor ratio
2. The production function can also be represented in per worker terms
a. 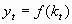
b. Can plot the per-worker production function assuming no productivity
growth.
Same shape as the original production function
3. Steady states
The steady state exists when the economy is growing at a constant rate.
In the Solow model this implies that here in no growth in productivity. We’ll
examine the conditions which underlie the steady state.
a. In the steady state the per-capita levels of output, capital and
consumption will be constant over time. (labor force and capital grow at
the same rate…)
b. Gross Investment must: Replace worn out capital, which decrease at
the depreciation rate (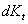 ) Expand so the
capital stock will grow as the economy grows (
) Expand so the
capital stock will grow as the economy grows (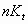 )
)
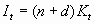
c. Substitute into the above expression for consumption
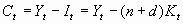
d. In per worker terms in the steady state
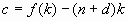
e. Plot c, f(k), and (n + d)k
f. Increasing k will increase c up to a point. After this point
c will decline.
4. Reaching the Steady State
a. Assume saving is dependent upon current income
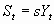 s is the saving rate between 0 and 1
s is the saving rate between 0 and 1
b. In closed economy Saving equals investment
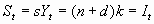
sf(k) = (n + d)k
c. Plot sf(k) and (n + d)k
d. kss is the only possible steady state capital labor ratio
it is where saving is equal to the steady state level of investment.
e. If k does not equal kss then the economy will converge to
the steady state level
if k<kss Then saving > investment
needed to keep k constant so k increases
if k>kss Then saving <
investment needed to keep k constant so k decreases
f. The economy reaches a long run steady state if there is no
productivity growth.
B. The fundamental determinants of long-run living standards
1. The Saving Rate
a. Higher saving rate leads to a higher capital labor ratio, higher
output per worker and consumption per worker depends on the golden rule.
b. Should policy increase the saving rate
May lower consumption in the short run, but will increase output per
worker
Trade-off between future and present consumption
2. Population Growth
a. Population growth lowers the capital output ratio, lowers
consumption per worker
b. Policy to lower population growth
Raises the consumption per worker
Reduce total output and consumption, lowering a nation’s
ability to defend itself or influence world events
c. The Solow model also assumes that the population of working age is
fixed may not be true as the population grows. Social security and
health care issues
3. Productivity growth
a. The key factor in determining economic growth – increase the
output worker for a giving level of capital labor ratio
b. In equilibrium, productivity improvements increase the capital
labor ratios, output per worker and consumption per worker
Increase in output per worker will increase the capital labor ratio
which will increase the supply of saving causing the long-run
capital-labor ration to rise
c. Is there a limit? Can consumption per worker grow indefinitely?
Saving rate cannot rise forever…population growth rate can not
fall forever…
However productivity and innovation can always occur, so living
standard can rise continuously
4. Do Economies converge?
a. Unconditional convergence
b. Conditional convergence
c. No convergence
d. Evidence and international financial markets
D. The new growth theory – Explaining the sources of productivity growth
1. Human Capital
a. Knowledge, skill and training
b. Richer countries invest in more human capital
c. Higher levels of human capital are linked to economic growth and output
per worker
2. Technological innovation
a. Research and development
b. Learning by doing
3. Policy issues
III. Government Policy to Raise Long Run Living Standards
A. Policies to affect the saving rate:
1. Should government try to change the saving rate? – Depends on
whether the saving market is efficient or not
2. How can saving be increased?
Raise interest rate, but in practice the response of saving to the real
interest rate appears to be small
Increase Government Saving
Reduce Deficit or Increase Surplus – difficult to do since it
requires taxes to increase or spending to decrease.
B. Improve Infrastructure:
1. US spending on infrastructure has decreased in the last 20 years
2. Does it increase productivity?
Do richer countries spend more on
infrastructure or does infrastructure increase a nations
wealth?
Decisions are political
3. Building Human Capital
4. Encouraging research and development
C. Industrial Policy
1. Should government intervene in allocating resources to productivity
enhancing industry?
![]() F(K,N) from Chapter
3
F(K,N) from Chapter
3= elasticity of output with respect to capital
= elasticity of output with respect to labor
and
are less than one due to diminishing marginal returns
and
from the data
?K/K and
?N/N