1.    I will be flexible on this problem.  First I know that some have calculated the problem with one tuition payment next year and some have done it with one this year and one next.  I will accept both.  Here is the method for one payment next year,  First, a general formulation of the problem is useful. With income of Y₁ in the first year and Y₂ in the second year, the consumer saves Y₁ – C in the first year and Y₂ – C in the second year, where C is the consumption amount, which is the same in both years. Saving in the first year earns interest at rate r, where r is the real interest rate. And the consumer needs to accumulate just enough after two years to pay for college tuition, in the amount T. So the key equation is (Y₁ – C)(1 + r) + (Y₂ – C) = T.

        (a)  Y₁ = Y₂ = $50,000, r = 10%, T = $12,600. The key equation gives ($50,000 – C)1.1 + ($50,000 – C) = $12,600. This can be simplified to $50,000 – C = $12,600/2.1 = $6000, which can be solved to get C = $44,000. Then S = Y – C = $50,000 – $44,000 = $6000.

        (b)  Y₁ = $54,200. The key equation is now ($54,200 – C)1.1 + ($50,000 – C) = $12,600. This can be simplified to ($54,200 ´ 1.1) + $50,000 – $12,600 = 2.1 C, or $97,020 = 2.1 C, so C = $46,200. Then S = Y₁ – C = $54,200 – $46,200 = $8000. This illustrates that a rise in current income increases saving.

        (c)  Y₂ = $54,200. The key equation is now ($50,000 – C)1.1 + ($54,200 – C) = $12,600. This can be simplified to ($50,000 ´ 1.1) + $54,200 – $12,600 = 2.1 C, or $96,600 = 2.1 C, so C = $46,000. Then S = Y₁ – C = $50,000 – $46,000 = $4000. This illustrates that a rise in future income decreases saving.

        (d)  With the increase in wealth of W, the total amount invested for the second period is W + Y₁ – C, so the key equation becomes ($1050 + $50,000 – C)1.1 + ($50,000 – C) = $12,600. This can be simplified to ($51,050 ´ 1.1) + $50,000 – $12,600 = 2.1 C, or $93,555 = 2.1 C, so C = $44,550. Then S = Y₁ – C = $50,000 – $44,550 = $5450. This illustrates that a rise in wealth decreases saving.

        (e)  T = $14,700. The key equation is now ($50,000 – C)1.1 + ($50,000 – C) = $14,700. This can be simplified to $50,000 – C = $14,700/2.1 = $7000, which can be solved to get C = $43,000. Then S = Y – C = $50,000 – $43,000 = $7000. The rise in targeted wealth needed in the future raises current saving.

        (f)  r = 25%. The key equation is now ($50,000 – C)1.25 + ($50,000 – C) = $12,600. This can be simplified to $50,000 – C = $12,600/2.25 = $5600, which can be solved to get C = $44,400. Then S = Y – C = $50,000 – $44,400 = $5600. The rise in the real interest rate, with a given wealth target, reduces current saving.

6.     (a)  S^d = Y – C^d – G

= Y – (3600 – 2000r + 0.1Y) – 1200

= –4800 + 2000r + 0.9Y

(b)  (1) Using Eq. (4.7): Y = C^d + I^d + G

Y = (3600 – 2000r + 0.1Y) + (1200 – 4000r) + 1200

= 6000 – 6000r + 0.1Y

So 0.9Y = 6000 – 6000r

At full employment, Y = 6000. Solving 0.9 ´ 6000 = 6000 – 6000r, we get r = 0.10.

(2) Using Eq. (4.8):

S^d = I^d

–4800 + 2000r + 0.9Y = 1200 – 4000r

0.9Y = 6000 – 6000r

When Y = 6000, r = 0.10.

So we can use either Eq. (4.7) or (4.8) to get to the same result.

        (c)  When G = 1440, desired saving becomes S^d = Y – C^d – G = Y – (3600 – 2000r + 0.1Y) – 1440 =
 –5040 + 2000r + 0.9Y. S^d is now 240 less for any given r and Y; this shows up as a shift in the S^d line from S¹ to S² in Figure 4.3.

Figure 4.3

Setting S^d = I^d, we get:

–5040 + 2000r + 0.9Y = 1200 – 4000r

6000r + 0.9Y = 6240

At Y = 6000, this is 6000r = 6240 – (0.9 ´ 6000) = 840, so r = 0.14. The market-clearing real interest rate increases from 10% to 14%.

7.     (a)  r = 0.10

uc/(1 – τ) = (r + d)p_K/(1 – t) = [(.1 + .2) ´ 1]/(1 – .5) = 0.6.

MPK^f = uc/(1 – t), so 20 – .02K^f = .6; solving this gives K^f = 970.

Since K^f – K = I – dK, I = K^f – K + dK = 970 – 900 + (.2 ´ 900) = 250.

        (b)  i.   Solving for this in general:

uc/(1 – t) = (r + d)p_K/(1 – τ) = [(r + .2) ´ 1]/(1 – .5) = .4 + 2r.

MPK^f = uc/(1 – t), so 20 – .02K = .4 + 2r; solving this gives K^f = 980 – 100r.

I = K^f – K + dK = 980 – 100r – 900 + (.2 ´ 900) = 260 – 100r.

              ii.  Y = C + I + G

1000 = [100 + (.5 ´ 1000) – 200r] +

(260 – 100r) + 200

1000 = 1060 – 300r, so 300r = 60

r = 0.2

C = 560; I = 240 = S;

uc/(1 – t) = .4 + (2 ´ .2) = 0.8;

K^f = 960

5.     When there is a temporary increase in government spending, consumers foresee future taxes. As a result, consumption declines, both currently and in the future. Thus current consumption does not fall by as much as the increase in G, so national saving (S^d = Y – C^d – G) declines at the initial real interest rate, and the saving curve shifts to the left from S¹ to S², as shown in Figure 4.15. Thus the real interest rate increases and consumption and investment both fall.

Figure 4.15

        When there is a permanent increase in government spending, consumers foresee future taxes as well, with both current and future consumption declining. But if there is an equal increase in current and future government spending, and consumers try to smooth consumption, they will reduce their current and future consumption by about the same amount, and that amount will be about the same amount as the increase in government spending. So the saving curve in the saving-investment diagram does not shift, and there is no change in the real interest rate.

        Since the saving curve shifts upward more in the case of a temporary increase in government spending, the real interest rate is higher, so investment declines by more. However, consumption falls by more in the case of a permanent increase in government spending.

4.    In any period, the net amount of new foreign assets that a country acquires equals its current account surplus, which in turn must equal its capital and financial account deficit. A country with greater net foreign assets than another is not necessarily better off. What really counts is total national wealth, which consists of both net foreign assets and net domestic assets. For example, the United States has lower net foreign assets than other countries, but has one of the world’s highest levels of total national wealth per citizen.

5.    In a small open economy, saving does not have to be equal to investment. Saving can be used to finance domestic investment or it can be lent abroad. So saving equals investment plus net exports.

       Similarly, output need not equal absorption. Absorption is a country’s total spending on consumption, investment, and government purchases. Absorption may be different from output because some output may be exported. The difference between output and absorption is net exports.

7.    In a world with two large open economies, the world real interest rate is determined such that desired international lending by one country equals desired international borrowing by the other country. When the world real interest rate is at its equilibrium value, the current accounts of the two countries sum to zero.

1.   

            Current account balance (CA) = 300 – 355 = –55.

            Net exports (NX) = (100 + 90) – (125 + 80) = –15.

       Notice that the increase in home reserve assets is just a subcategory of the increase in home country assets, so it is not included separately. Similarly, the increase in foreign reserve assets is just a subcategory of the increase in foreign assets in the home country. The information about the changes in home and foreign reserve assets is included for calculation of the official settlements balance only; it does not affect the capital and financial account.

           Capital and financial account balance (KFA) = 200 – 160 = 40.

           Statistical discrepancy (SD):

           CA + KFA + SD = 0

            –55 + 40 + SD = 0

           SD = 15

            Official settlements balance = increase in home official reserve assets minus increase in foreign official reserve assets = 30 – 35 = –5.

3.         All variables but interest rates are in billions of dollars.

        (a)  S = 10 + (100 ´ 0.03) = 13

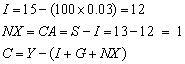
A = C + I + G

= 27 + 12 + 10

= 49

        (b)  S = 13, as before.

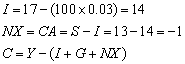
4.     (a)  To find the equilibrium interest rate (r^w), we must first calculate the current account for each country as a function of r^w. Then we can find the value of r^w that clears the goods market, that is, where CA + CA_For = 0.

Home:

C^d = 320 + 0.4(1000 – 200) – 200r^w

= 320 + 320 – 200 r^w

= 640 – 200 r^w

CA = NX = S^d – I^d = Y – (C^d + I^d + G)

= 1000 – (640 – 200 r^w + 150 – 200r^w + 275)

= –65 + 400 r^w

Foreign:

= 480 + 0.4(1500 - 300) - 300r^w

= 480 + 480 – 300r^w

= 960 – 300r^w

CA_For = NX_For = S^d_For – I^d_For = Y_For – (C^d_For + I^d_For + G_For)

= 1500 – (960 – 300r^w + 225 – 300r^w + 300)

= 15 + 600 r^w

At equilibrium, CA + CA_For = 0, so:

–65 + 400 r^w + 15 + 600 r^w = 0

–50 + 1000 r^w = 0

r^w = .05

C = 640 – 200 r^w = 630

C_For = 960 – 300 r^w = 945

S = Y – C – G = 1000 – 630 – 275 = 95

S_For = Y_For – C_For – G_For = 1500 – 945 – 300 = 255

I = 150 – 200 r^w = 140

I_For = 225 – 300 r^w = 210

CA = S – I = 95 – 140 = –45

CA_For = S_For – I_For = 255 – 210 = 45

        (b)  C^d = 320 + 0.4(1000 – 250) – 200 r^w

= 320 + 300 – 200 r^w

= 620 – 200 r^w

CA = NX = S^d – I^d = Y – (C^d + I^d + G)

= 1000 – (620 – 200 r^w + 150 – 200 r^w + 325)

= –95 + 400 r^w

At equilibrium, CA + CA_For = 0, so:

–95 + 400 r^w + 15 + 600 r^w = 0

–80 + 1000 r^w = 0

r^w = 0.08

C = 620 – 200 r^w = 604

C_For = 960 – 300 r^w = 936

S = Y – C – G = 1000 – 604 – 325 = 71

S_For = Y_For – C_For – G_For = 1500 – 936 – 300 = 264

I = 150 – 200 r^w = 134

I_For = 225 – 300 r^w = 201

CA = S – I = 71 – 134 = –63

CA_For = S_For – I_For = 264 – 201 = 63

So a balanced-budget increase in government spending increases the home country’s current account deficit.