Untitled 1

2. (a) This chart shows the MPK^f as the increase in output from adding another fabricator:

# Fabricators	Output	MPK^f
0	0	—
1	100	100
2	150	50
3	180	30
4	195	15
5	205	10
6	210	5

(b) uc  (r  d)p_K  (0.12  0.20)$100  $32. HHHHC should buy two fabricators, since at two fabricators, MPK^f  50  32  uc. But at three fabricators, MPK^f  30  32  uc. You want to add fabricators only if the future marginal product of capital exceeds the user cost of capital. The MPK^f of the third fabricator is less than its user cost, so it should not be added.

MPK^f  30  28  uc for the third fabricator and MPK^f  15  28  uc for the fourth fabricator.

(d) With taxes, they should add additional fabricators as long as (1 – )MPK^f  uc. Since   0.4,
1 –   0.6. They should buy just one fabricator, since (1 – )MPK^f  0.6 ´ 100  60  32  uc. They shouldn’t buy two, since then (1 – τ)MPK^f  0.6 ´ 50  30  32  uc.

(e) When output doubles, the MPK^f doubles as well. At r  0.12, they should buy three fabricators, since then MPK^f  60  32  uc; they shouldn’t buy four, since then MPK^f  30  32  uc.

At r  0.08, they should buy four fabricators, since then MPK^f  30  28  uc; they shouldn’t buy five, since then MPK^f  20  28  uc.

4. Since the price of capital declines from 60 to 51, the depreciation rate is 9/60  .15.

(a) uc  (r  d)p_K  (.10  .15)60  15 units of output per year.

(b) The desired capital stock is such that MPK^f  uc, so 165 – 2K  15, or 2K  150, so K  75.

(c) The tax-adjusted user cost of capital is uc/(1 – ), so with   .4, the condition for the desired capital stock is 165 – 2K  15/0.6, or 2K  140; the solution is K  70. Thus taxation decreases the firm’s desired capital stock.

(d) I wrestled with the best way to handle this. I decide that it is best to look at an investment tax credit as basically lowering the price of capital from 60 to (1 – 0.2)60  48. So the tax-adjusted user cost of capital is only (.25 ´ 48)/0.6  20. Then the equation for setting the desired capital stock is 165 – 2K  20, or 2K  145; the solution is K  72.5. Thus the investment tax credit increases the firm’s desired capital stock. Several ask me about this problem and I gave none a good answer so I will be very flexible on this part.

6. (a) S^d  Y – C^d – G

 Y – (3600 – 2000r  0.1Y) – 1200

 –4800  2000r  0.9Y

(b) (1) Using Eq. (4.7): Y  C^d  I^d  G

Y  (3600 – 2000r  0.1Y)  (1200 – 4000r)  1200

 6000 – 6000r  0.1Y

So 0.9Y  6000 – 6000r

At full employment, Y  6000. Solving 0.9 ´ 6000  6000 – 6000r, we get r  0.10.

(2) Using Eq. (4.8):

S^d  I^d

–4800  2000r  0.9Y  1200 – 4000r

0.9Y  6000 – 6000r

When Y  6000, r  0.10.

So we can use either Eq. (4.7) or (4.8) to get to the same result.

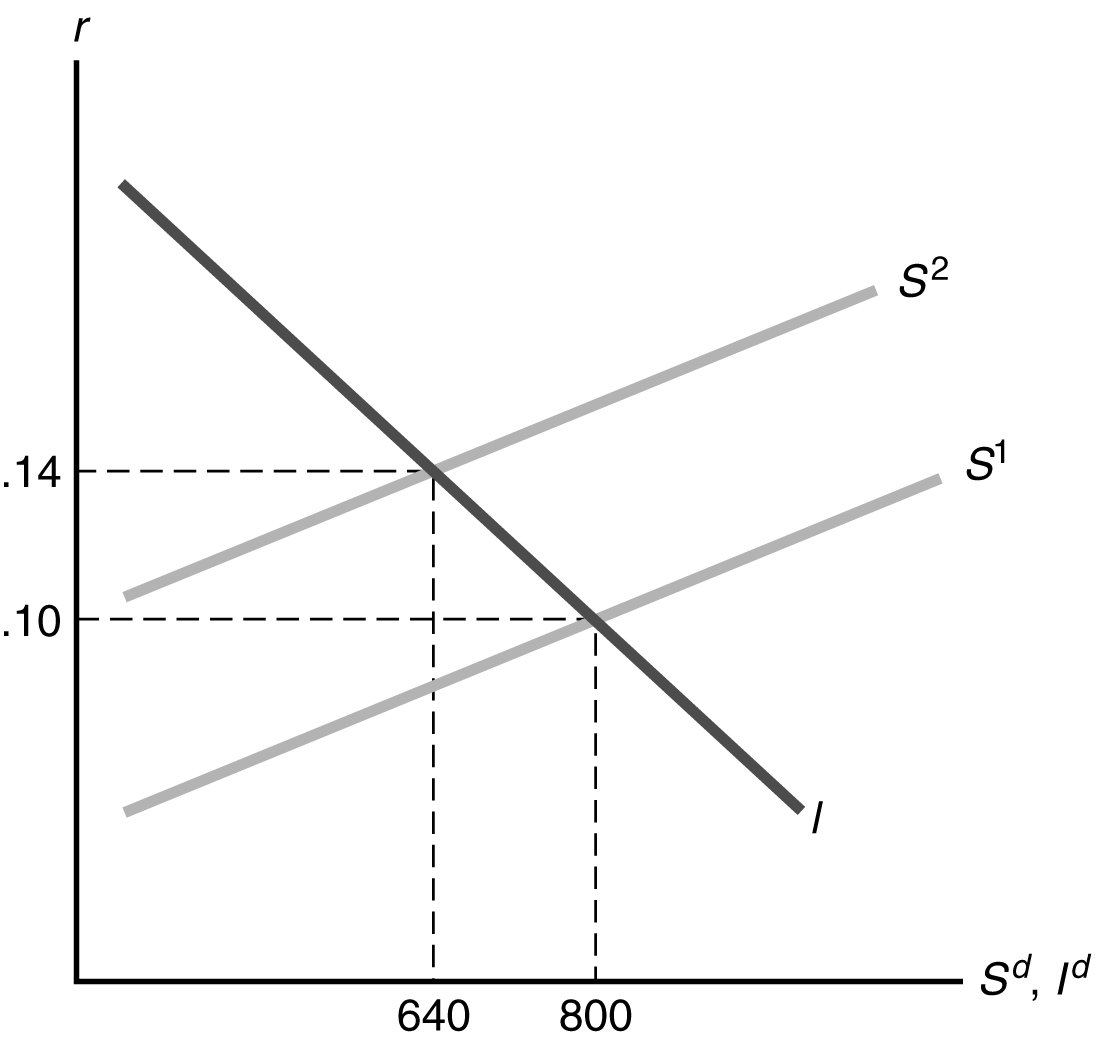
(c) When G  1440, desired saving becomes S^d  Y – C^d – G  Y – (3600 – 2000r  0.1Y) – 1440  –5040  2000r  0.9Y. S^d is now 240 less for any given r and Y; this shows up as a shift in the S^d line from S¹ to S² in Figure 4.3.

Setting S^d  I^d, we get:

–5040  2000r  0.9Y  1200 – 4000r

6000r  0.9Y  6240

At Y  6000, this is 6000r  6240 – (0.9 ´ 6000)  840, so r  0.14. The market-clearing real interest rate increases from 10% to 14%.

7. (a) r  0.10

uc/(1 – τ)  (r  d)p_K/(1 – )  [(.1  .2) ´ 1]/(1 – .5)  0.6.

MPK^f  uc/(1 – ), so 20 – .02K^f  .6; solving this gives K^f  970.

Since K^f – K  I – dK, I  K^f – K  dK  970 – 900  (.2 ´ 900)  250.

(b) i. Solving for this in general:

uc/(1 – )  (r  d)p_K/(1 – τ)  [(r  .2) ´ 1]/(1 – .5)  .4  2r.

MPK^f  uc/(1 – ), so 20 – .02K  .4  2r; solving this gives K^f  980 – 100r.

I  K^f – K  dK  980 – 100r – 900  (.2 ´ 900)  260 – 100r.

ii. Y  C  I  G

1000  [100  (.5 ´ 1000) – 200r] 

(260 – 100r)  200

1000  1060 – 300r, so 300r  60

r  0.2

C  560; I  240  S;

uc/(1 – )  .4  (2 ´ .2)  0.8;

K^f  960

1. (a) As Figure 4.5 shows, the shift to the right in the saving curve from S¹ to S² causes saving and investment to increase and the real interest rate to decrease.

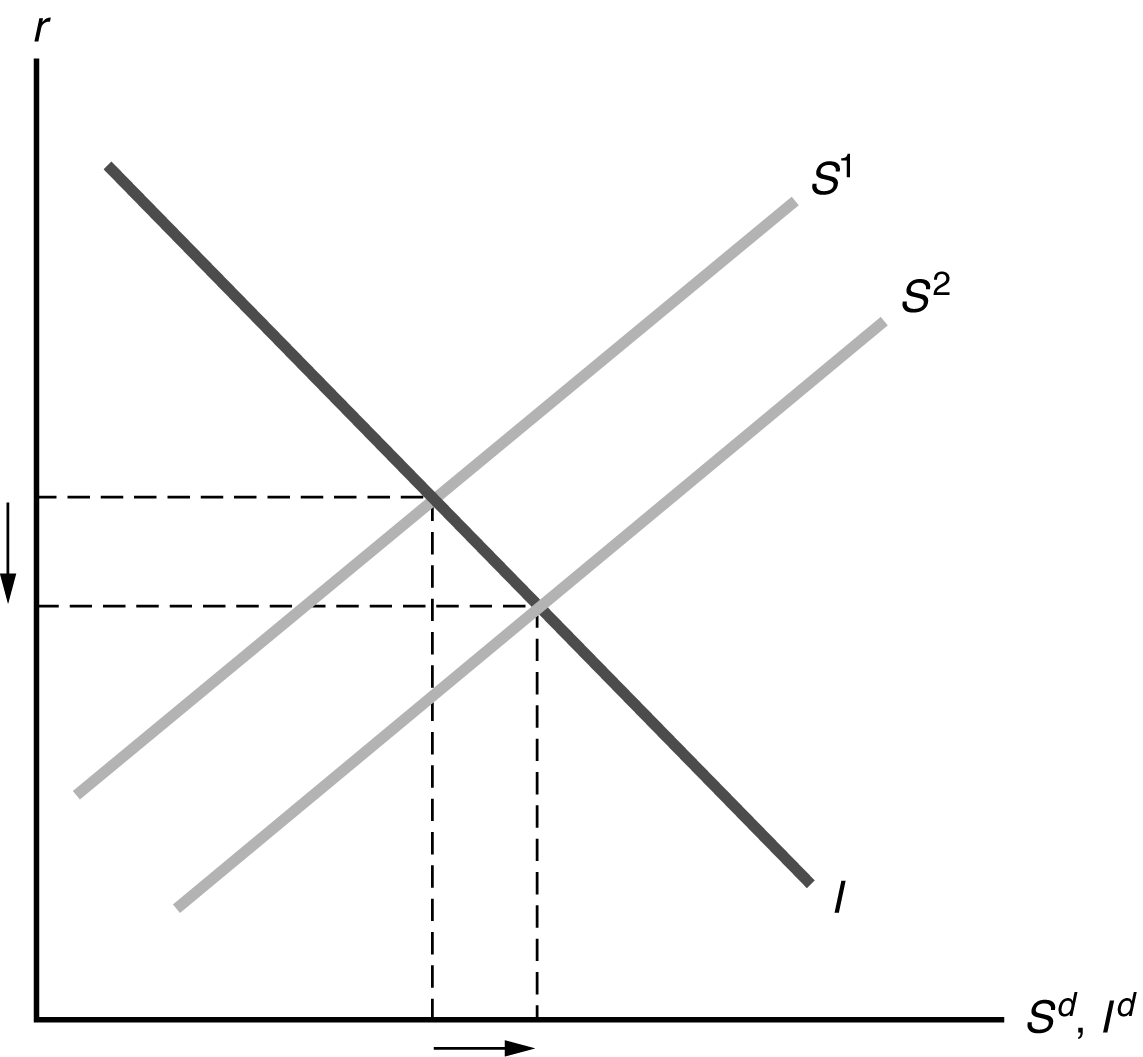
Figure 4.5

(b) This is really just a transfer from the general population to veterans. The effect on saving depends on whether the marginal propensity to consume (MPC) of veterans differs from that of the general population. If there is no difference in MPCs, there will be no shift of the saving curve; neither investment nor the real interest rate is affected. If the MPC of veterans is higher than the MPC of the general population, then desired national saving declines and the saving curve shifts to the left; the real interest rate rises and investment declines. If the MPC of veterans is lower than that of the general population, the saving curve shifts to the right; the real interest rate declines and investment rises.

(c) The investment tax credit encourages investment, shifting the investment curve from I¹ to I² in Figure 4.6. Saving and investment increase, as does the real interest rate.

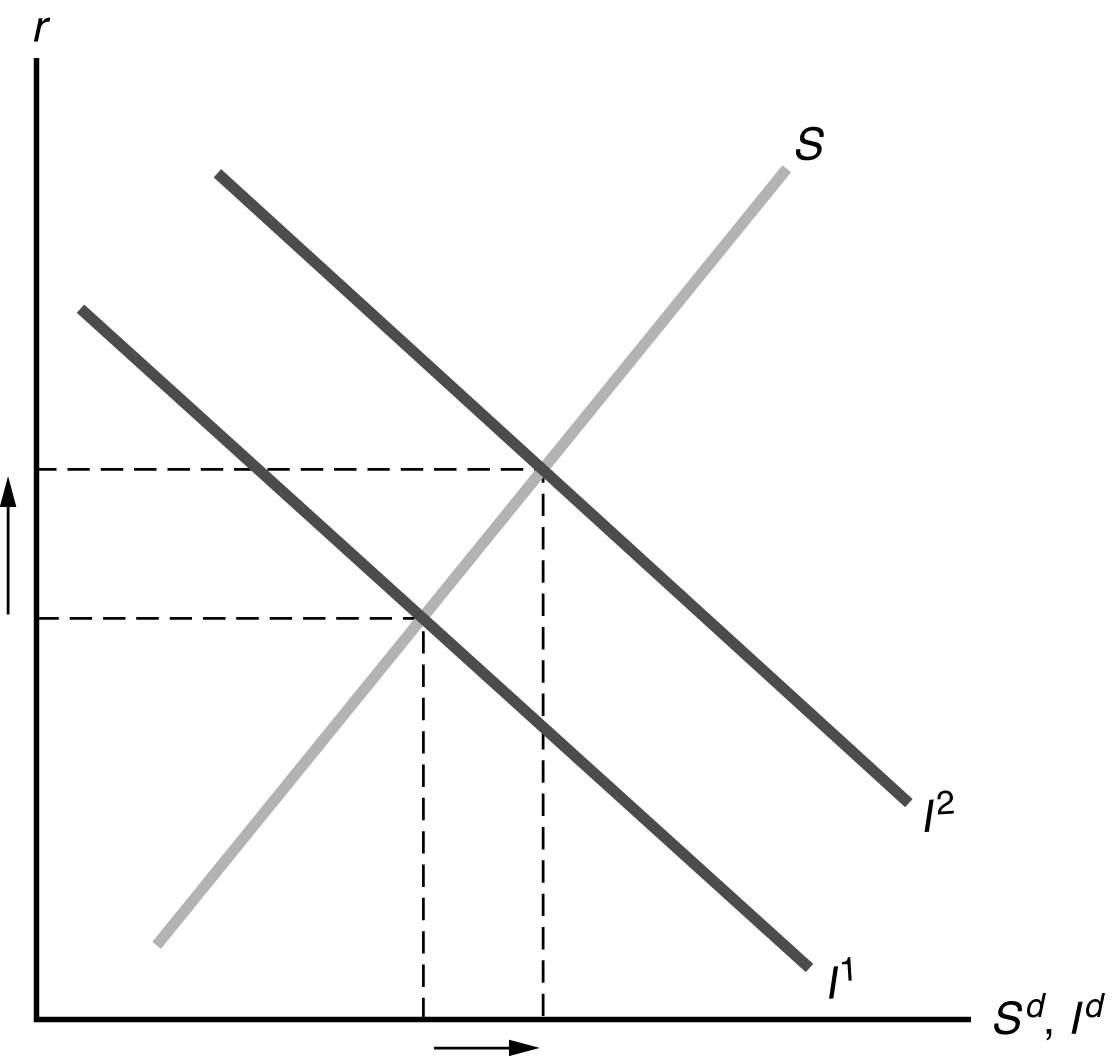
Figure 4.6

(d) The increase in expected future income decreases current desired saving, as people increase desired consumption immediately. The rise of the future marginal productivity of capital shifts the investment curve to the right. The result, as shown in Figure 4.7, is that the real interest rate rises, with ambiguous effects on saving and investment.

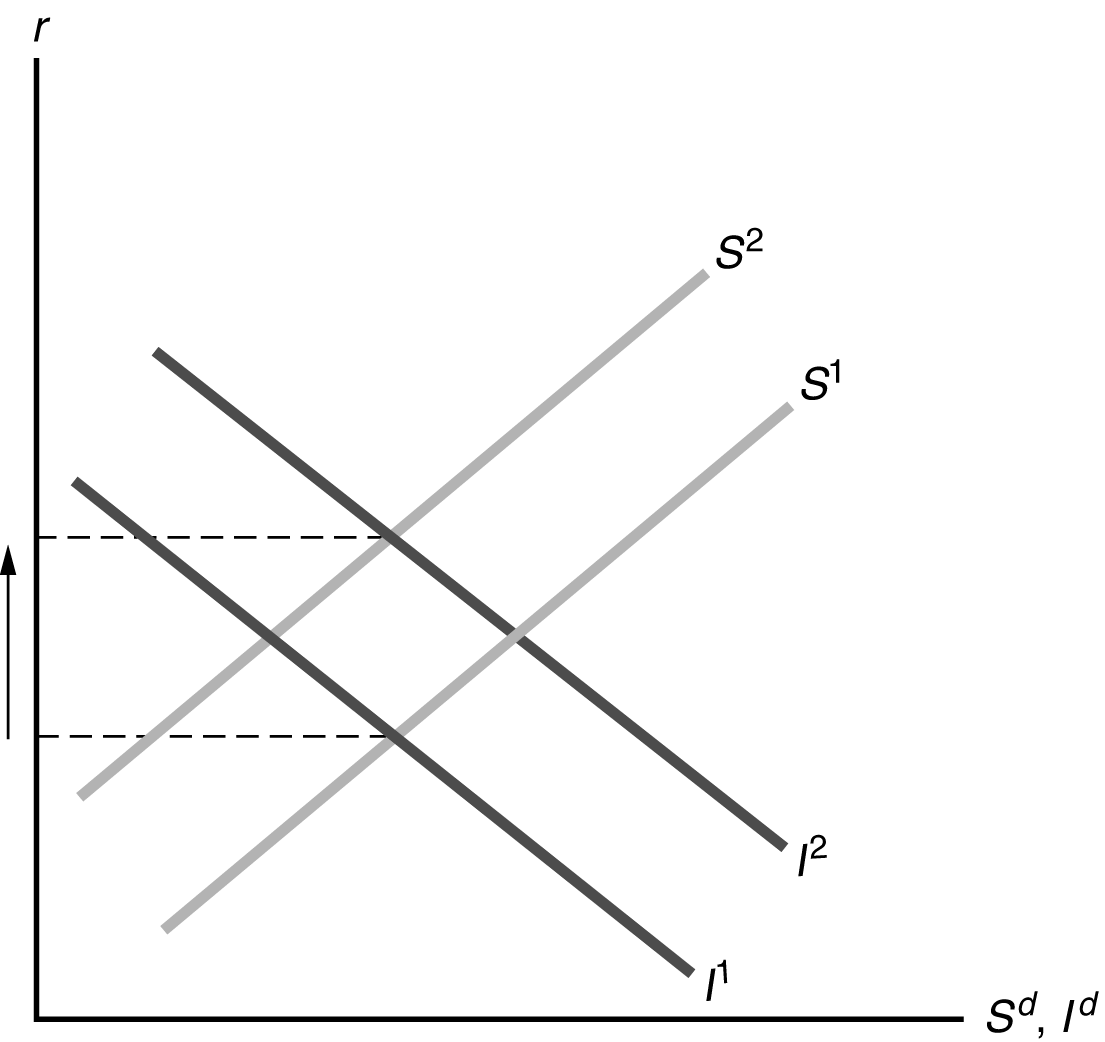
Figure 4.7

2. (a) With a lower capital stock, the marginal product of labor is reduced, so the labor demand curve shifts to the left from ND¹ to ND² in Figure 4.8. Then the new equilibrium point is one with lower employment and a lower real wage. With lower employment and a lower capital stock, full-employment output will be lower.

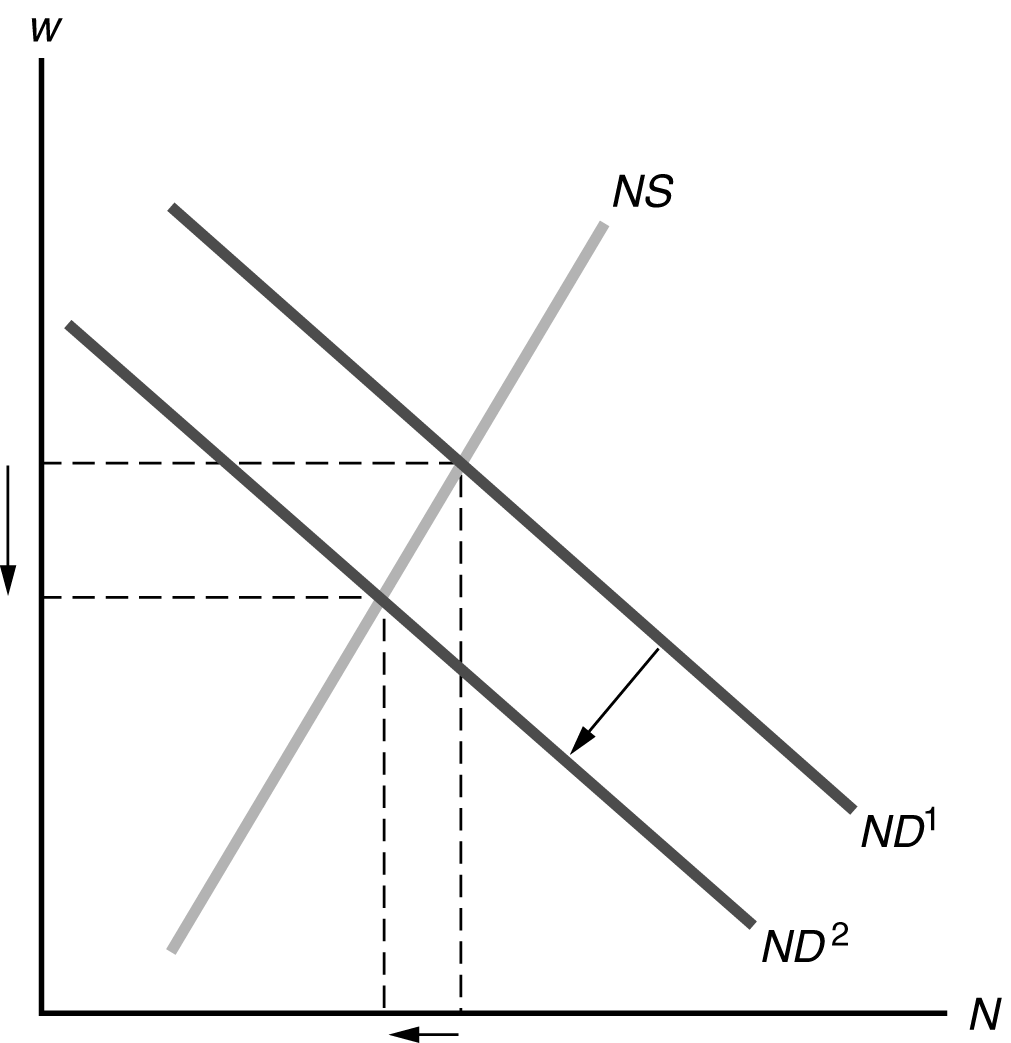
Figure 4.8

(b) Because the capital stock is lower, the marginal product of capital will be higher, so desired investment will increase.

(c) Since current output declines, desired saving declines, because people do not want to reduce their consumption. On the other hand, since future output is also lower, people desire to save more today to make up for the loss of future income.

(d) The increase in desired investment shows up as a shift to the right in the I^d curve, from I¹ to I² in Figure 4.9. Then the new equilibrium (assuming no change in desired saving) is at a higher level of investment and a higher real interest rate.

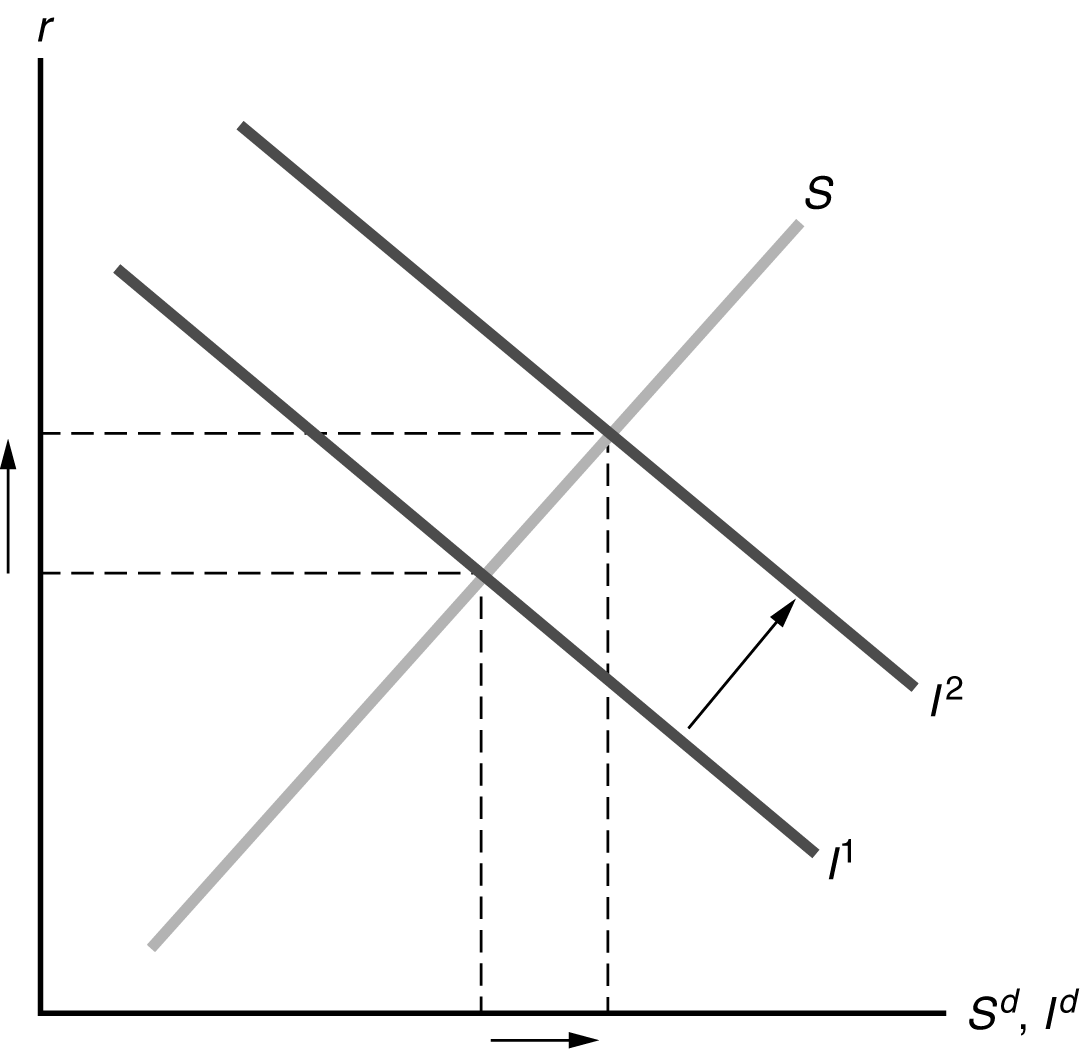
Figure 4.9