
1. Hula hoop fabricators cost $100 each. The Hi-Ho hula Hoop Company is trying
to decide how many of these machines to buy. HHHHC expects to produce the
following numbers of hoops each year for each level of capital stock shown.
Number
of Fabricators Number
of Hoops
Produced per Year
0 0
1 100
2 150
3 180
4 195
5 205
6 210
Hula hoops have a real value of $1 each. HHHHC has no other costs besides the
cost of fabricators.
a. Find
the expected future marginal product of capital (in terms of dollars) for each
level of capital. The MPKf for
the third fabricator, for example, is the real value of the extra output
obtained when the third fabricator is added
(a) This chart shows the
MPKf as the increase in
output from adding another fabricator:
|
#
Fabricators |
Output |
MPKf |
|
0 |
0 |
— |
|
1 |
100 |
100 |
|
2 |
150 |
50 |
|
3 |
180 |
30 |
|
4 |
195 |
15 |
|
5 |
205 |
10 |
|
6 |
210 |
5 |
b. If
the real interest rate is 12% per year and the depreciation rate of capital is
20% per year, find the user cost of capital (in dollars per fabricator per
year). How many fabricators should HHHHC buy?
(b)
uc
= (r
+
d)pK
= (0.12
+ 0.20)$100
= $32.
HHHHC should buy two fabricators,
since at two fabricators, MPKf
= 50
> 32 =
uc. But at three fabricators,
MPKf
= 30
< 32 =
uc. You want to add fabricators only
if the future marginal product of capital exceeds the user cost of capital. The
MPKf
of the third fabricator is less than its user cost, so it should not be added.
c. Repeat
Part (b) for a real interest rate of 8% per year
(c)
When r
= 0.08,
uc
= (0.08 + 0.20)$100
= $28. Now they should buy three
fabricators, since
MPKf
=
30 >
28
=
uc
for the third fabricator and MPKf
=
15
<
28
=
uc
for the fourth fabricator.
d. Repeat
Part (b) for a 40% tax on HHHHC’s sales revenues.
(d)
With taxes, they should add additional fabricators as long as (1
-
t)MPKf
>
uc. Since
t
= 0.4, 1
-
t
= 0.6. They should buy just one
fabricator, since (1 -
t)MPKf
= 0.6
´
100 = 60
> 32
= uc. They shouldn’t buy two,
since then (1 -
τ)MPKf
= 0.6
´
50 = 30
< 32
= uc.
e. A
technical innovation doubles the number of hoops a fabricator can produce. How
many fabricators should HHHHC buy when the real interest rate is 12% per year?
8% per year? Assume that there are no taxes and that the depreciation rate is
still 20% per year.
(e)
When output doubles, the MPKf
doubles as well. At r
= 0.12, they should buy three
fabricators, since then MPKf
= 60
> 32 =
uc; they shouldn’t buy four, since
then MPKf
= 30
< 32 =
uc.
At
r =
0.08, they should buy four fabricators, since then
MPKf
= 30
> 28 =
uc; they shouldn’t buy five, since
then MPKf
= 20
< 28 =
uc.
2. An economy has full-employment output of 6000. Government purchases, G, are
1200. Desired consumptions and desired investment are
Cd =3600
– 2000r + 0.10Y, and
Id =
1200 – 4000r,
Where Y is output and r is the real interest rate.
a. Find
an equation relating desired national saving, Sd, to r and Y
(a)
Sd
=
Y -
Cd
-
G
=
Y -
(3600 - 2000r
+ 0.1Y)
- 1200
= -4800
+ 2000r
+ 0.9Y
b. Using
both versions of the goods market equilibrium conditions, Eqs. (4.7) and (4.8),
find the real interest rate that clears the good market. Assume that output
equals full-employment output.
(b)
(1) Using Eq. (4.7): Y
=
Cd
+
Id
+
G
Y =
(3600 - 2000r
+ 0.1Y)
+ (1200
- 4000r)
+ 1200
= 6000
- 6000r
+ 0.1Y
So 0.9Y
= 6000
- 6000r
At full employment, Y = 6000.
Solving 0.9
´
6000 = 6000
- 6000r, we get r
= 0.10.
(2) Using
Eq. (4.8):
Sd =
Id
-4800
+
2000r
+
0.9Y
=
1200 -
4000r
0.9Y
=
6000 -
6000r
When Y
=
6000, r =
0.10.
So we can use either Eq. (4.7) or (4.8) to get to the same result.
c. Government
purchases rise to 1440. How does this increase change the equation describing
desired national saving? Show the change graphically. What happens to the
market-clearing real interest rate?
(c) When
G =
1440, desired saving becomes Sd
=
Y -
Cd
-
G =
Y -
(3600 - 2000r
+ 0.1Y)
- 1440
= -5040
+ 2000r
+ 0.9Y.
Sd is now 240 less
for any given r and
Y; this shows up as a shift in the
Sd line from
S1 to
S2 in the Figure

Figure
Setting Sd = Id,
we get:
-5040
+ 2000r
+ 0.9Y
= 1200
- 4000r
6000r
+ 0.9Y
= 6240
At Y
= 6000, this is 6000r
= 6240
- (0.9
´
6000) = 840, so r
= 0.14. The market-clearing real
interest rate increases from 10% to 14%.
3. Suppose that the economywide expected future marginal product of capital is
MPKf = 20 – 0.02K,
where K is the future capital stock. The depreciation rate of capital, d,
is 20% per period. The current capital stock is 900 units of capital. The price
of a unit of capital is 1 unit of output. Firms pay taxes equal to 50% of their
output. The consumption function in the economy is C= 100 + 0.5Y-200r, where C
is consumption, Y is output, and r is the real interest rate. Government
purchases equal 200, and full-employment output is 1000.
a.
suppose that the real interest rate is 10% per period. What are the values of
the tax-adjusted user cost of capital, the desired future capital stock, and the
desired level of investment?
(a)
r =
0.10
uc/(1
-
τ)
= (r
+
d)pK/(1
-
t)
= [(.1
+ 0.2)
´
1]/(1 - 0.15)
= 0.35.
MPKf
=
uc/(1
-
t),
so 20 - 0.02K
= 0.35; solving this gives
K
= 982.5.
Since
K
-
K-1
=
I
-
dK, I
=
K -
K-1
+
dK = 982.5
- 900
+ (.2
´
900) = 262.5.
b. Now
consider the real interest rate determined by goods market equilibrium. This
part of the problem will guide you to this interest rate.
i.
Write the tax-adjusted user cost of capital as a function of the real interest
rate r. also write the desired future capital stock and desired investment as
functions of r.
ii.
Use the investment function derived in Part (i) along with the consumption
function and government purchases, to calculate the real interest rate that
clears the goods market. What are the goods market-clearing values of
consumption, saving, and investment? What are the tax-adjusted user cost of
capital and the desired capital stock in this equilibrium?
(b) i.
Solving for this in general:
uc/(1
-
t)
= (r
+
d)pK/(1
-
τ)
= [(r
+
.2)
´
1]/(1 - 0.15)
= .235
+ 1.176r.
MPKf
=
uc/(1
-
t),
so 20 - 0.02K
= 0.235
+ 1.176r;
solving this gives
K
= 988.25
- 58.8r.
I =
K -
K-1
+
dK = 988.25
- 58.8r
- 900
+ (0.2
´
900) = 268.25
- 58.8r.
ii. Y
= C
+ I
+ G
1000 = [100
+ (.5
´
1000) - 200r]
+ (268.25
- 58.8r)
+ 200
1000 = 1068.25
- 258.8r,
so 258.8r
= 68.25
r =
0.264
C =
100 + (0.5
´
1000) - (200 × 0.264) = 547.2
I = 268.25
- (58.8 × 0.264) = 252.7 =
S
uc/(1
-
t)
= 0.235 + (1.176
´
0.264) = 0.545
K
= 988.25 - (58.8 × 0.264) = 972.7
4. Use the
saving-investment diagram to analyze the effects of the following on national
saving, investment, and the real interest rate. Explain your reasoning.
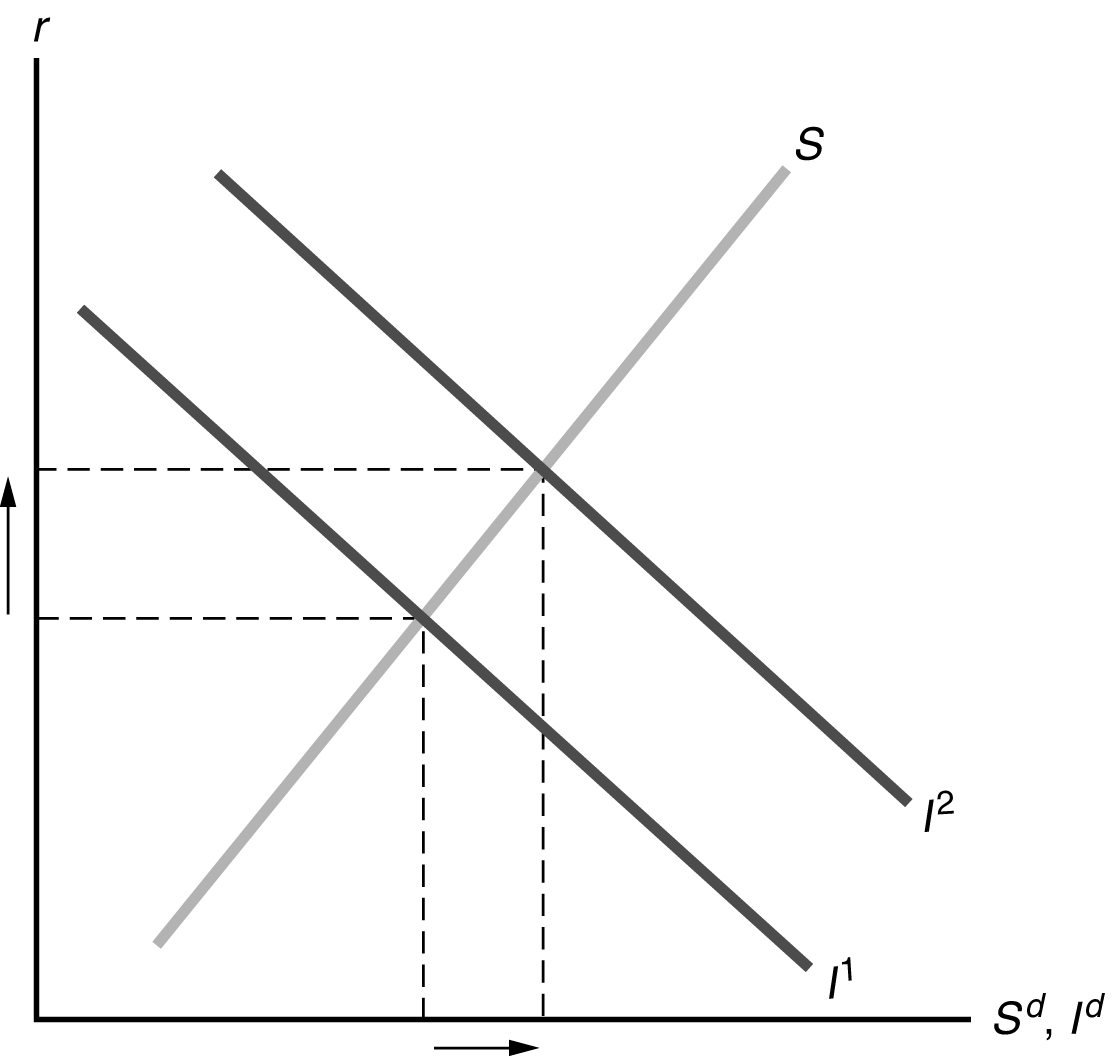
a. Consumers
become more future-oriented and thus decide to save more.
b. The
government announces a large, one-time bonus payment to veterans returning from
a war. The bonus will be financed by additional taxes levied on the general
population over the next five years.
c. The
government introduces an investment tax credit (offset by other types of taxes,
so total tax collections remain unchanged).
d. A
large number of accessible oil deposits are discovered, which increases the
expected future marginal product of oil rigs and pipelines. It also causes an
increases in expected future income.
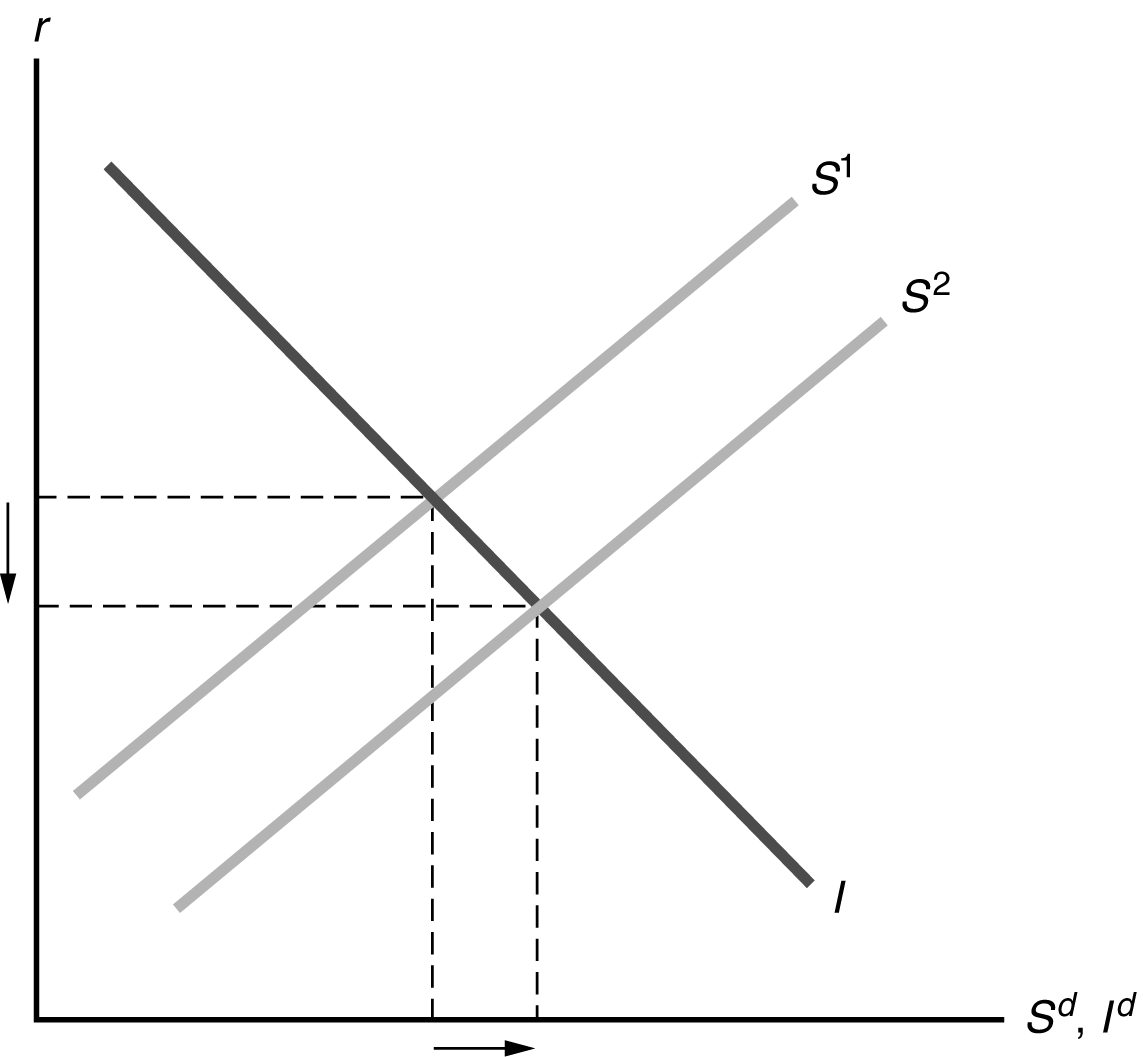
The
increase in expected future income decreases current desired saving, as people
increase desired consumption immediately. The rise of the future marginal
productivity of capital shifts the investment curve to the right. The result, as
shown in Figure, is that the real interest rate rises, with ambiguous effects on
saving and investment.

5. A country loses much
of its capital stock to a war.
e. What
effects should this event have on the country’s current employment, output, and
real wage?

f. What
effect will the loss of capital have on desired investment
Because the capital stock is lower, the marginal product of capital will be
higher, so desired investment will increase.
g. The
effects of desired national saving of the wartime losses are ambiguous. Give one
reason for desired saving to rise and one reason for it to fall.
(c)
Since current output declines, desired saving declines, because people do
not want to reduce their consumption. On the other hand, since future output is
also lower, people desire to save more today to make up for the loss of future
income.
h. Assume
that desired saving doesn’t change. What effect does the loss of capital have on
the country’s real interest rate and the quantity of investment?

6. In a small open
economy, output (gross domestic product) is $25 billion, government purchases
are $6 billion, and net factor payments from abroad are zero. Desired
consumption and desired investment are related to the world real interest rate
in the following manner:
World Real Interest Rate Desired
Consumption Desired
Investment
5% $12
billion $3
billion
4% $13
billion $4
billion
3% $14
billion $5
billion
2% $15
billion $6
billion
For each
value of the world real interest rate, find national saving, foreign lending,
and absorption. Calculate net exports as the difference between output and
absorption. What is the relationship between net exports and foreign lending?
The following table calculates key variables for this question for different
values of the real interest rate. The column for S is calculated by the
equation S = Y
- (Cd
+ G). The column headed S
- I is foreign lending.
Absorption (A) is Cd
+ Id + G.
Net exports (NX) are output (Y) minus absorption (A). Every
column except r consists of dollar amounts in billions.
|
r |
Cd |
Id |
S |
S -
I |
A |
NX |
|
5% |
12 |
3 |
7 |
4 |
21 |
4 |
|
4% |
13 |
4 |
6 |
2 |
23 |
2 |
|
3% |
14 |
5 |
5 |
0 |
25 |
0 |
|
2% |
15 |
6 |
4 |
–2 |
27 |
–2 |
Net exports and foreign lending are identical.
3. All variables
but interest rates are in billions of dollars.
(a) S
= 10
+ (100
´
0.03) = 13
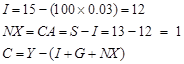
![]()
A
= C
+ I
+ G
=
27 + 12
+ 10
=
49
(b) S
= 13, as before.
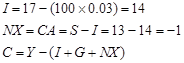
![]()
![]()
![]()