1. The central limit theorem suggests that when the sample
size (![]() ) is
large, the distribution of the sample average (
) is
large, the distribution of the sample average (![]() )
is approximately
)
is approximately ![]() with
with ![]() Given a
population
Given a
population ![]()
![]() we have
we have
(a)
![]()
![]() and
and
![]()
(b)
![]()
![]() and
and
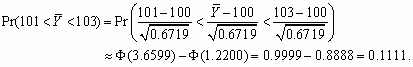
(c)
![]()
![]() and
and
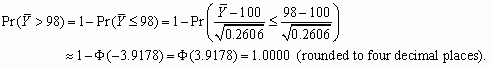
3. Denote each voter’s preference by
![]()
![]() if the voter
prefers the incumbent and
if the voter
prefers the incumbent and
![]() if the voter
prefers the challenger.
if the voter
prefers the challenger.
![]() is a Bernoulli
random variable with probability Pr
is a Bernoulli
random variable with probability Pr![]() and Pr
and Pr![]() From the
solution to Exercise 3.2,
From the
solution to Exercise 3.2,
![]() has mean
has mean
![]() and variance
and variance
![]()
(a)
![]()
(b)
![]() The standard error is SE
The standard error is SE![]()
(c) The computed t-statistic is
![]()
Because of the large sample size
![]() we can use Equation (3.14) in the text to get
the
we can use Equation (3.14) in the text to get
the
p-value for the test
![]() vs.
vs.
![]()
![]()
(d) Using Equation (3.17) in the text, the
p-value for the test
![]() vs.
vs.
![]() is
is
![]()
(e) Part (c) is a two-sided test and the p-value is the area in the tails of the standard normal distribution outside ± (calculated t-statistic). Part (d) is a one-sided test and the p-value is the area under the standard normal distribution to the right of the calculated t-statistic.
(f) For the test
![]() vs.
vs.
![]() we cannot reject the null hypothesis at the 5%
significance level. The p-value 0.066 is
larger than 0.05. Equivalently the calculated
t-statistic
we cannot reject the null hypothesis at the 5%
significance level. The p-value 0.066 is
larger than 0.05. Equivalently the calculated
t-statistic
![]() is less than the critical value 1.645 for a
one-sided test with a 5% significance level. The
test suggests that the survey did not contain
statistically significant evidence that the
incumbent was ahead of the challenger at the
time of the survey.
is less than the critical value 1.645 for a
one-sided test with a 5% significance level. The
test suggests that the survey did not contain
statistically significant evidence that the
incumbent was ahead of the challenger at the
time of the survey.
4. Using Key Concept 3.7 in the text
(a) 95% confidence interval for p is
![]()
(b) 99% confidence interval for p is
![]()
(c) The interval in (b) is wider because of a larger critical value due to a lower significance level.
(d) Since 0.50 lies inside the 95% confidence interval for p, we cannot reject the null hypothesis at a 5% significance level.
12. Sample size for men
![]() sample average
sample average
![]() sample standard
deviation
sample standard
deviation ![]() Sample size for women
Sample size for women
![]() sample average
sample average
![]() sample standard
deviation
sample standard
deviation ![]() The
standard error of
The
standard error of
![]() is SE
is SE![]()
(a) The hypothesis test for the difference in mean monthly salaries is
![]()
The t-statistic for testing the null hypothesis is
![]()
Use Equation (3.14) in the text to get the p-value:
![]()
The extremely low level of p-value implies that the difference in the monthly salaries for men and women is statistically significant. We can reject the null hypothesis with a high degree of confidence.
(b) From part (a), there is overwhelming statistical evidence that mean earnings for men differ from mean earnings for women. To examine whether there is gender discrimination in the compensation policies, we take the following one-sided alternative test
![]()
With the t-statistic
![]() the p-value for the one-sided test is:
the p-value for the one-sided test is:
![]()
With the extremely small p-value, the null hypothesis can be rejected with a high degree of confidence. There is overwhelming statistical evidence that mean earnings for men are greater than mean earnings for women. However, by itself, this does not imply gender discrimination by the firm. Gender discrimination means that two workers, identical in every way but gender, are paid different wages. The data description suggests that some care has been taken to make sure that workers with similar jobs are being compared. But, it is also important to control for characteristics of the workers that may affect their productivity (education, years of experience, etc.). If these characteristics are systematically different between men and women, then they may be responsible for the difference in mean wages. (If this is true, it raises an interesting and important question of why women tend to have less education or less experience than men, but that is a question about something other than gender discrimination by this firm.) Since these characteristics are not controlled for in the statistical analysis, it is premature to reach a conclusion about gender discrimination.
1. (a)
Average Hourly Earnings, Nominal $’s
|
Mean |
SE(Mean) |
95% Confidence Interval |
|
|
AHE1992 |
11.63 |
0.064 |
11.50 11.75 |
|
AHE2004 |
16.77 |
0.098 |
16.58 16.96 |
|
Difference |
SE(Difference) |
95% Confidence Interval |
|
|
AHE2004 AHE1992 |
5.14 |
0.117 |
4.91 5.37 |
(b)
Average Hourly Earnings, Real $2004
|
Mean |
SE(Mean) |
95% Confidence Interval |
|
|
AHE1992 |
15.66 |
0.086 |
15.49 15.82 |
|
AHE2004 |
16.77 |
0.098 |
16.58 16.96 |
|
Difference |
SE(Difference) |
95% Confidence Interval |
|
|
AHE2004 AHE1992 |
1.11 |
0.130 |
0.85 1.37 |
(c) The results from part (b) adjust for changes in purchasing power. These results should be used.
(d)
Average Hourly Earnings in 2004
|
Mean |
SE(Mean) |
95% Confidence Interval |
|
|
High School |
13.81 |
0.102 |
13.61 14.01 |
|
College |
20.31 |
0.158 |
20.00 20.62 |
|
Difference |
SE(Difference) |
95% Confidence Interval |
|
|
College High School |
6.50 |
0.188 |
6.13 6.87 |
(e)
Average Hourly Earnings in 1992 (in $2004)
|
Mean |
SE(Mean) |
95% Confidence Interval |
|
|
High School |
13.48 |
0.091 |
13.30 13.65 |
|
College |
19.07 |
0.148 |
18.78 19.36 |
|
Difference |
SE(Difference) |
95% Confidence Interval |
|
|
College High School |
5.59 |
0.173 |
5.25 5.93 |
(f)
Average Hourly Earnings in 2004
|
Mean |
SE(Mean) |
95% Confidence Interval |
|
|
AHEHS,2004 AHEHS,1992 |
0.33 |
0.137 |
0.06 0.60 |
|
AHECol,2004 AHECol,1992 |
1.24 |
0.217 |
0.82 1.66 |
|
Col–HS Gap (1992) |
5.59 |
0.173 |
5.25 5.93 |
|
Col–HS Gap (2004) |
6.50 |
0.188 |
6.13 6.87 |
|
Difference |
SE(Difference) |
95% Confidence Interval |
|
|
Gap2004 Gap1992 |
0.91 |
0.256 |
0.41 1.41 |
Wages of high school graduates increased by an estimated 0.33 dollars per hour (with a 95% confidence interval of 0.06
0.60); Wages of college graduates increased by an estimated 1.24 dollars per hour (with a 95% confidence interval of 0.82 1.66). The College High School gap increased by an estimated 0.91 dollars per hour.(g) Gender Gap in Earnings for High School Graduates
|
Year |
|
sm |
nm |
|
sw |
nw |
|
SE( |
95% CI |
|
1992 |
14.57 |
6.55 |
2770 |
11.86 |
5.21 |
1870 |
2.71 |
0.173 |
2.37 3.05 |
|
2004 |
14.88 |
7.16 |
2772 |
11.92 |
5.39 |
1574 |
2.96 |
0.192 |
2.59 3.34 |
There is a large and statistically
significant gender gap in earnings for high
school graduates.
In 2004 the estimated gap was $2.96 per hour; in
1992 the estimated gap was $2.71 per hour
(in $2004). The increase in the gender gap is
somewhat smaller for high school graduates than
it is for college graduates.